题目内容
若函数y=ax+b(a>0,a≠1)的图象过P(0,0)与Q(1,9)两点,设函数f(x)=loga(x+b).
(1)若函数g(x)=f(x)+f(x+m+1)在区间[2,+∞)上是单调递增的,求实数m的取值范围;
(2)令h(x)=f(2x)+f(2x+1),不等式h(x)>lgk对任意的x∈[1,2]恒成立,求实数k的取值范围.
(1)若函数g(x)=f(x)+f(x+m+1)在区间[2,+∞)上是单调递增的,求实数m的取值范围;
(2)令h(x)=f(2x)+f(2x+1),不等式h(x)>lgk对任意的x∈[1,2]恒成立,求实数k的取值范围.
考点:指数函数的图像与性质
专题:计算题,函数的性质及应用
分析:(1)由题意得到方程组
,从而解出a、b;代入得到g(x)=lg(x-1)+lg(x+m),从而求实数m的取值范围;
(2)易知h(x)=lg(2x-1)+lg(2x)在[1,2]上是增函数,恒成立问题化成最值问题.
|
(2)易知h(x)=lg(2x-1)+lg(2x)在[1,2]上是增函数,恒成立问题化成最值问题.
解答:
解:(1)由题意,
,
解得,a=10,b=-1,
则f(x)=lg(x-1),
则g(x)=lg(x-1)+lg(x+m),
∵g(x)=lg(x-1)+lg(x+m)在区间[2,+∞)上是单调递增的,
∴由二次函数的图象可知,m<2,
(2)h(x)=lg(2x-1)+lg(2x)在[1,2]上是增函数,
则h(x)min=h(1)=lg2,
则不等式h(x)>lgk对任意的x∈[1,2]恒成立可化为
lg2>lgk,
则0<k<2.
|
解得,a=10,b=-1,
则f(x)=lg(x-1),
则g(x)=lg(x-1)+lg(x+m),
∵g(x)=lg(x-1)+lg(x+m)在区间[2,+∞)上是单调递增的,
∴由二次函数的图象可知,m<2,
(2)h(x)=lg(2x-1)+lg(2x)在[1,2]上是增函数,
则h(x)min=h(1)=lg2,
则不等式h(x)>lgk对任意的x∈[1,2]恒成立可化为
lg2>lgk,
则0<k<2.
点评:本题考查了指数函数与对数函数的性质应用,属于基础题.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
已知向量
、
、
是单位向量,且
•
=0,则(
-
)•(
-
)的最大值为( )
| a |
| b |
| c |
| a |
| b |
| a |
| c |
| b |
| c |
A、
| ||
B、2+
| ||
C、
| ||
D、
|
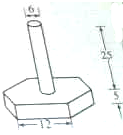 如图是一种机器零件,零件下面是六棱柱(底面是正 六边形,侧面是全等的矩形)形.上面是圆柱(尺寸如图,单位:mm),电镀这种零件需要用锌,已知每平方米用锌0.11kg,问电镀10000个零件需锌多少千克(结果精确到0.01kg).
如图是一种机器零件,零件下面是六棱柱(底面是正 六边形,侧面是全等的矩形)形.上面是圆柱(尺寸如图,单位:mm),电镀这种零件需要用锌,已知每平方米用锌0.11kg,问电镀10000个零件需锌多少千克(结果精确到0.01kg).