题目内容
14.已知命题p:“函数$f(x)={2^{{x^2}-2x}}+{m^2}-\frac{5m}{2}+\frac{1}{2}$在R上有零点”,命题q:函数f(x)=$\frac{2}{x-m}$在区间(1,+∞)内是减函数,若p∧q为真命题,则实数m的取值范围为[$\frac{1}{2}$,1].分析 分别求出p,q为真时的m的范围,根据若p∧q为真命题,取交集即可.
解答 解:函数$f(x)={2^{{x^2}-2x}}+{m^2}-\frac{5m}{2}+\frac{1}{2}$在R上有零点,
即-${2}^{{x}^{2}-2x}$=m2-$\frac{5m}{2}$+$\frac{1}{2}$有解,
令g(x)=-${2}^{{x}^{2}-2x}$≤-$\frac{1}{2}$,
故m2-$\frac{5m}{2}$+$\frac{1}{2}$≤-$\frac{1}{2}$,
解得:$\frac{1}{2}$≤m≤2;
故p为真时:m∈[$\frac{1}{2}$,2];
函数f(x)=$\frac{2}{x-m}$在区间(1,+∞)内是减函数,
则m≤1,
若p∧q为真命题,则p真q真,
故$\frac{1}{2}≤m≤1$,
故答案为:[$\frac{1}{2}$,1].
点评 本题考查了复合命题的判断,考查指数函数以及二次函数的性质,是一道中档题.

练习册系列答案
相关题目
4.已知函数f(x)的定义域为R,M为常数.若p:对?x∈R,都有f(x)≥M;q:M是函数f(x)的最小
值,则p是q的( )
值,则p是q的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
2.参加成都七中数学选修课的同学,对某公司的一种产品销量与价格进行了统计,得到如下数据和散点图:
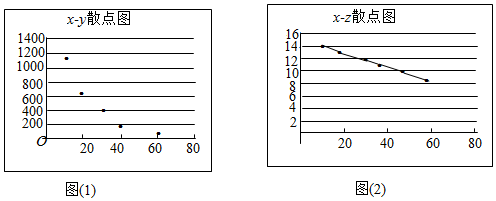
(参考数据:$\sum_{i=1}^6{({x_i}-\overline x)}•({y_i}-\overline y)=-34580$,$\sum_{i=1}^6{({x_i}-\overline x)}•({z_i}-\overline z)=-175.5$$\sum_{i=1}^6{{{({y_i}-\overline y)}^2}}=776840$,$\sum_{i=1}^6{({y_i}-\overline y)}•({z_i}-\overline z)=3465.2$)
(1)根据散点图判断,y与x,z与x哪一对具有较强的线性相关性(给出判断即可,不必说明理由)?
(2)根据(1)的判断结果及数据,建立y关于x的回归方程(方程中的系数均保留两位有效数字).
(3)定价为多少元/kg时,年利润的预报值最大?
附:对于一组数据(x1,y1),(x2,y2),(x3,y3),…,(xn,yn),其回归直线$\widehat{y}$=$\widehat{b}$•x+$\widehat{a}$的斜率和截距的最小二乘估计分别为:
$\widehat{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})•({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n•\overline{x}•\overline{y}}{\sum_{i=1}^{n}{x}_{i}^{2}-n•\stackrel{-2}{x}}$,$\widehat{a}$=$\overline{y}$-n•$\widehat{b}$•$\overline{x}$.

| 定价x(元/kg) | 10 | 20 | 30 | 40 | 50 | 60 |
| 年销量y(kg) | 1150 | 643 | 424 | 262 | 165 | 86 |
| z=2lny | 14.1 | 12.9 | 12.1 | 11.1 | 10.2 | 8.9 |
(1)根据散点图判断,y与x,z与x哪一对具有较强的线性相关性(给出判断即可,不必说明理由)?
(2)根据(1)的判断结果及数据,建立y关于x的回归方程(方程中的系数均保留两位有效数字).
(3)定价为多少元/kg时,年利润的预报值最大?
附:对于一组数据(x1,y1),(x2,y2),(x3,y3),…,(xn,yn),其回归直线$\widehat{y}$=$\widehat{b}$•x+$\widehat{a}$的斜率和截距的最小二乘估计分别为:
$\widehat{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})•({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n•\overline{x}•\overline{y}}{\sum_{i=1}^{n}{x}_{i}^{2}-n•\stackrel{-2}{x}}$,$\widehat{a}$=$\overline{y}$-n•$\widehat{b}$•$\overline{x}$.