题目内容
3.已知函数f(x)=b+logax(x>0且a≠1)的图象经过点(8,2)和(1,-1).(1)求f(x)的解析式;
(2)[f(x)]2=3f(x),求实数x的值;
(3)令y=g(x)=2f(x+1)-f(x),求y=g(x)的最小值及其最小值时x的值.
分析 (1)由已知得b+loga8=2,b+loga1=-1,从而求解析式即可;
(2)[f(x)]2=3f(x),即f(x)=0或3,即可求实数x的值;
(3)化简g(x)=2[log2(x+1)-1]-(log2x-1)=log2(x+$\frac{1}{x}$+2)-1,从而利用基本不等式求最值.
解答 解:(1)由已知得,b+loga8=2,b+loga1=-1,(a>0且a≠1),
解得a=2,b=-1;
故f(x)=log2x-1(x>0);
(2)[f(x)]2=3f(x),即f(x)=0或3,
∴log2x-1=0或3,
∴x=2或16;
(3)g(x)=2f(x+1)-f(x)
=2[log2(x+1)-1]-(log2x-1)=log2(x+$\frac{1}{x}$+2)-1≥1,
当且仅当x=$\frac{1}{x}$,即x=1时,等号成立).
于是,当x=1时,g(x)取得最小值1.
点评 本题考查了对数的运算及对数函数的应用,同时考查了基本不等式的应用.

练习册系列答案
相关题目
11.设全集U=Z,集合A={x|1≤x<7,x∈Z},B={x=2k-1,k∈Z},则A∩(∁UB)=( )
| A. | {1,2,3,4,5,6} | B. | {1,3,5} | C. | {2,4,6} | D. | ∅ |
2.不等式|x2-2|<2的解集是( )
| A. | (-2,0)∪(0,2) | B. | (-2,2) | C. | (-1,0)∪(0,1) | D. | (-1,1) |
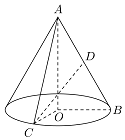 如图,在Rt△AOB中,$∠OAB=\frac{π}{6}$,斜边AB=4,D是AB中点,现将Rt△AOB以
如图,在Rt△AOB中,$∠OAB=\frac{π}{6}$,斜边AB=4,D是AB中点,现将Rt△AOB以