题目内容
4.已知在二项式${(\root{3}{x}-\frac{1}{{2\root{3}{x}}})^n}$的展开式中,第6项为常数项.(1)求n的值,并求含x2项的系数;
(2)求展开式中所有的有理项.
分析 (1)利用通项公式即可得出.
(2)根据通项公式,由题意得$\left\{\begin{array}{l}\frac{10-2r}{3}∈Z\\ 0≤r≤10,r∈Z.\end{array}$,令$\frac{10-2r}{3}$=k(k∈Z),r=5-$\frac{3}{2}$k.对k取值即可得出.
解答 解:(1)通项公式为Tr+1=Cnr${x}^{\frac{n-r}{3}}$(-$\frac{1}{2}$)r${x}^{-\frac{r}{3}}$=Cnr(-$\frac{1}{2}$)rx${x}^{\frac{n-2r}{3}}$.
∵第6项为常数项,∴r=5时,有$\frac{n-2r}{3}$=0,即n=10.
令$\frac{n-2r}{3}$=2,得r=$\frac{1}{2}$(n-6)=2.
∴所求的x2项的系数为C102(-$\frac{1}{2}$)2=$\frac{45}{4}$.
(2)根据通项公式,由题意得$\left\{\begin{array}{l}\frac{10-2r}{3}∈Z\\ 0≤r≤10,r∈Z.\end{array}$,
令$\frac{10-2r}{3}$=k(k∈Z),则10-2r=3k,即r=5-$\frac{3}{2}$k.
∵r∈Z,∴k应为偶数.
∴k可取2,0,-2,即r可取2,5,8.
∴第3项,第6项与第9项为有理项,它们分别为C102(-$\frac{1}{2}$)2x2,C105(-$\frac{1}{2}$)5,C108(-$\frac{1}{2}$)8x-2.
点评 本题考查了二项式定理的性质及其应用、分类讨论方法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
19.已知a,b∈R,则“ab>0“是“$\frac{b}{a}$+$\frac{a}{b}$>2”的( )
| A. | 充分非必要条件 | B. | 必要非充分条件 | ||
| C. | 充要条件 | D. | 既非充分也非必要条件 |
16.设集合P={x|0≤x≤4},Q={y|0≤y≤4},能表示集合P到集合Q的函数关系的有( )


| A. | ①②③④ | B. | ①②③ | C. | ②③ | D. | ② |
2.不等式|x2-2|<2的解集是( )
| A. | (-2,0)∪(0,2) | B. | (-2,2) | C. | (-1,0)∪(0,1) | D. | (-1,1) |
3.曲线y=$\frac{x}{x+1}$+lnx在点(1,$\frac{1}{2}$)处的切线方程为( )
| A. | y=$\frac{5}{4}$x+$\frac{3}{4}$ | B. | y=$\frac{5}{4}$x-$\frac{3}{4}$ | C. | y=-$\frac{5}{4}$x-$\frac{3}{4}$ | D. | y=-$\frac{5}{4}$x+$\frac{3}{4}$ |
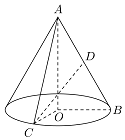 如图,在Rt△AOB中,$∠OAB=\frac{π}{6}$,斜边AB=4,D是AB中点,现将Rt△AOB以
如图,在Rt△AOB中,$∠OAB=\frac{π}{6}$,斜边AB=4,D是AB中点,现将Rt△AOB以