题目内容
19．
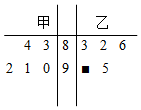如图的茎叶图表示的是甲、乙两人在5天内加工零件的个数，其中一个数字不小心被污损，已知甲的平均数等于乙的平均数，则污损的数字是（ ）| A． | 5 | B． | 1 | C． | 3 | D． | 4 |
分析 由茎叶图求出甲的平均成绩是88，设污损数字为x，乙的平均成绩为87.2+$\frac{x}{5}$，由题意知88=87.2+$\frac{x}{5}$，由此能求出甲的平均成绩等于乙的平均成绩时的x．
解答 解：由已知中的茎叶图可得
甲的5次综合测评中的成绩分别为83，84，90，91，92，
则甲的平均成绩：$\frac{1}{5}$（83+84+90+91+92）=88，
设污损数字为x
则乙的5次综合测评中的成绩分别为83，82，86，95，90+x
则乙的平均成绩：$\frac{1}{5}$（83+82+86+95+90+x）=87.2+$\frac{x}{5}$，
∵甲的平均成绩等于乙的平均成绩，
∴88=87.2+$\frac{x}{5}$，解得x=4；
故选：D．
点评 本题考查概率的求法，是基础题，解题时要认真审题，注意茎叶图的合理运用．
练习册系列答案
云南师大附小一线名师提优作业系列答案
冲刺100分单元优化练考卷系列答案
相关题目
9．已知a，b，c，d∈R，给出下列四个命题，其中正确的是（ ）
| A． | 若a＞b，c＞d，则a-d＜b-c | B． | 若ac2＞bc2，则a＞b | ||
| C． | 若c＜b＜a，且ac＜0，则cb2＜ab2 | D． | 若a＞b，则lg（a-b）＞0 |
10．已知数列{an}满足an+an-1=n（-1）${\;}^{\frac{n（n+1）}{2}}$，Sn是其前n项和，若S2017=-1007-b，且a1b＞0，则$\frac{1}{{a}_{1}}$+$\frac{2}{b}$的最小值为（ ）
| A． | 3-2$\sqrt{2}$ | B． | 3 | C． | 2$\sqrt{2}$ | D． | 3$+2\sqrt{2}$ |
7．“x≠y”是“|x|≠|y|”的（ ）
| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充要条件 | D． | 既不充分也不必要条件 |
14．已知Sn为等差数列{an}的前n项和，给出下列两个命题：
命题p：若S3，S9都大于9，则S6大于11
命题q：若S6不小于12，则S3，S9中至少有1个不小于9．
那么，下列命题为真命题的是（ ）
命题p：若S3，S9都大于9，则S6大于11
命题q：若S6不小于12，则S3，S9中至少有1个不小于9．
那么，下列命题为真命题的是（ ）
| A． | ￢p | B． | （￢p）∧（￢q） | C． | p∧q | D． | p∧（￢q） |
4．已知函数f（x）=sin（ωx-ωπ）（ω＞0）的最小正周期为π，则f（$\frac{π}{12}$）等于（ ）
| A． | $\frac{1}{2}$ | B． | -$\frac{1}{2}$ | C． | $\frac{\sqrt{3}}{2}$ | D． | -$\frac{\sqrt{3}}{2}$ |
11．已知集合A={-1，0，1，2，3}，B={-1，0，1}，则A∩B的子集的个数为（ ）
| A． | 16 | B． | 15 | C． | 8 | D． | 7 |
8．已知函数f（x）=sin（2x+$\frac{π}{4}$），则下列结论中正确的是（ ）
| A． | 函数f（x）的最小正周期为2π | |
| B． | 函数f（x）的图象关于点（$\frac{π}{4}$，0）对称 | |
| C． | 由函数f（x）的图象向右平移$\frac{π}{8}$个单位长度可以得到函数y=sin2x的图象 | |
| D． | 函数f（x）在区间（$\frac{π}{8}$，$\frac{5π}{8}$）上单调递增 |
9．设全集U={x∈N*|x≤5}，A={1，4}，B={4，5}，则∁U（A∩B）=（ ）
| A． | {1，2，3，5} | B． | {1，2，4，5} | C． | {1，3，4，5} | D． | {2，3，4，5} |