题目内容
4.已知函数f(x)=sin(ωx-ωπ)(ω>0)的最小正周期为π,则f($\frac{π}{12}$)等于( )| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | -$\frac{\sqrt{3}}{2}$ |
分析 由已知利用周期公式可求ω的值,进而利用诱导公式,特殊角的三角函数值即可计算得解.
解答 解:∵由题意可得:ω=$\frac{2π}{π}$=2,
∴f($\frac{π}{12}$)=sin(2×$\frac{π}{12}$-2π)=sin$\frac{π}{6}$=$\frac{1}{2}$.
故选:A.
点评 本题主要考查了三角函数周期公式,诱导公式,特殊角的三角函数值在三角函数化简求值中的应用,属于基础题.

练习册系列答案
相关题目
15.已知向量$\overrightarrow{a}$=(1,2),$\overrightarrow{b}$=(2,t),且$\overrightarrow{a}$•$\overrightarrow{b}$=0,则|$\overrightarrow{b}$|=( )
| A. | $\sqrt{5}$ | B. | 2$\sqrt{2}$ | C. | 2$\sqrt{5}$ | D. | 5 |
16.过点(2,0)且圆心为(1,0)的圆的方程是( )
| A. | x2+y2+2x=0 | B. | x2+y2-2x=0 | C. | x2+y2-4x=0 | D. | x2+y2+4x=0 |
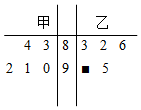 如图的茎叶图表示的是甲、乙两人在5天内加工零件的个数,其中一个数字不小心被污损,已知甲的平均数等于乙的平均数,则污损的数字是( )
如图的茎叶图表示的是甲、乙两人在5天内加工零件的个数,其中一个数字不小心被污损,已知甲的平均数等于乙的平均数,则污损的数字是( )