题目内容
14.已知Sn为等差数列{an}的前n项和,给出下列两个命题:命题p:若S3,S9都大于9,则S6大于11
命题q:若S6不小于12,则S3,S9中至少有1个不小于9.
那么,下列命题为真命题的是( )
| A. | ¬p | B. | (¬p)∧(¬q) | C. | p∧q | D. | p∧(¬q) |
分析 由等差数列的前n项和的性质可得:S3,S6-S3,S9-S6成等差数列,即可判断出命题p,q的真假.
解答 解:对于命题p:由等差数列的前n项和的性质可得:S3,S6-S3,S9-S6成等差数列,∴2(S6-S3)=S3+S9-S6,∴3S6=3S3+S9≥3×9+9,∴S6≥12,因此命题p正确;
命题q:由上面可知:3S3+S9=3S6≥3×12=36,因此S3,S9中至少有1个不小于9,是真命题.
那么,下列命题为真命题的是p∧q.
故选:C.
点评 本题考查了等差数列的前n项和的性质、复合命题真假的判定方法、不等式的性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案
相关题目
2.等比数列{an}中,a3=16,a5=4,则a7=( )
| A. | 1 | B. | -1 | C. | ±1 | D. | $\frac{1}{4}$ |
9.实数x,y满足条件$\left\{\begin{array}{l}{x≥1}\\{x+y≤3}\\{-2x+3y+5≥0}\end{array}\right.$,则目标函数z=x+2y的最大值为( )
| A. | 5 | B. | 4 | C. | -1 | D. | $\frac{16}{5}$ |
6.已知集合A={x|x2-2x-8>0},B={-3,-1,1,3,5},则A∩B=( )
| A. | {-1,1,3} | B. | {-3,-1,1} | C. | {-3,5} | D. | {3,5} |
3.若复数z满足(1+2i)•z=|2-i|,则$\overline{z}$( )
| A. | 1+2i | B. | $\sqrt{5}$(1-2i) | C. | $\frac{\sqrt{5}}{5}$(1+2i) | D. | $\frac{\sqrt{5}}{5}$(1-2i) |
4.下列命题是假命题的是( )
| A. | ?φ∈R,函数f(x)=sin(2x+φ)都不是偶函数 | |
| B. | ?α,β∈R,使cos(α+β)=cosα+cosβ | |
| C. | 向量$\overrightarrow a$=(-2,1),$\overrightarrow b$=(-3,0),则$\overrightarrow a$在$\overrightarrow b$方向上的投影为2 | |
| D. | “|x|≤1”是“x<1”的既不充分也不必要条件 |
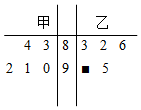 如图的茎叶图表示的是甲、乙两人在5天内加工零件的个数,其中一个数字不小心被污损,已知甲的平均数等于乙的平均数,则污损的数字是( )
如图的茎叶图表示的是甲、乙两人在5天内加工零件的个数,其中一个数字不小心被污损,已知甲的平均数等于乙的平均数,则污损的数字是( )