题目内容
11.已知集合A={-1,0,1,2,3},B={-1,0,1},则A∩B的子集的个数为( )| A. | 16 | B. | 15 | C. | 8 | D. | 7 |
分析 由A与B,求出两集合的交集,确定出交集子集个数即可.
解答 解:∵A={-1,0,1,2,3},B={-1,0,1},
∴A∩B={-1,0,1},
则A∩B的子集的个数为23=8,
故选:C.
点评 此题考查了交集及其运算,熟练掌握交集的定义是解本题的关键.

练习册系列答案
相关题目
1.已知在双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$中,F1,F2分别是左右焦点,A1,A2,B1,B2分别为双曲线的实轴与虚轴端点,若以A1A2为直径的圆总在菱形F1B1F2B2的内部,则此双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$离心率的取值范围是( )
| A. | $(1,\frac{{1+\sqrt{5}}}{2})$ | B. | [$\frac{1+\sqrt{5}}{2}$,+∞) | C. | $(1,\frac{{1+\sqrt{3}}}{2})$ | D. | $(\frac{{1+\sqrt{3}}}{2},+∞)$ |
2.等比数列{an}中,a3=16,a5=4,则a7=( )
| A. | 1 | B. | -1 | C. | ±1 | D. | $\frac{1}{4}$ |
6.已知集合A={x|x2-2x-8>0},B={-3,-1,1,3,5},则A∩B=( )
| A. | {-1,1,3} | B. | {-3,-1,1} | C. | {-3,5} | D. | {3,5} |
16.过点(2,0)且圆心为(1,0)的圆的方程是( )
| A. | x2+y2+2x=0 | B. | x2+y2-2x=0 | C. | x2+y2-4x=0 | D. | x2+y2+4x=0 |
3.若复数z满足(1+2i)•z=|2-i|,则$\overline{z}$( )
| A. | 1+2i | B. | $\sqrt{5}$(1-2i) | C. | $\frac{\sqrt{5}}{5}$(1+2i) | D. | $\frac{\sqrt{5}}{5}$(1-2i) |
1.已知O为△ABC的外心,|$\overrightarrow{AB}$|=16,|$\overrightarrow{AC}$|=10$\sqrt{2}$,若$\overrightarrow{AO}$=x$\overrightarrow{AB}$+y$\overrightarrow{AC}$,且32x+25y=25,则∠B=( )
| A. | $\frac{π}{3}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{6}$ | D. | $\frac{π}{12}$ |
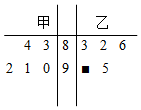 如图的茎叶图表示的是甲、乙两人在5天内加工零件的个数,其中一个数字不小心被污损,已知甲的平均数等于乙的平均数,则污损的数字是( )
如图的茎叶图表示的是甲、乙两人在5天内加工零件的个数,其中一个数字不小心被污损,已知甲的平均数等于乙的平均数,则污损的数字是( )