题目内容
ABCD-A1B1C1D1是一个边长为1的正方体，过顶点A作正方体的截面（该截面与正方体的表面不重合），若截面的形状为四边形，则截面面积的取值范围是
(1，
]
| 2 |
(1，
]
．| 2 |
分析：如图所示，设过顶点A作正方体的截面AEFG与底面ABCD所成的角为θ，利用关系式：
=cosθ，得出S截面AEFG＞1又当截面AEFG是正方体的对角面AB1C1D时，其面积最大，最大为
，从而得到截面面积的取值范围．
| S 底面ABCD |
| S 截面AEFG |
| 2 |
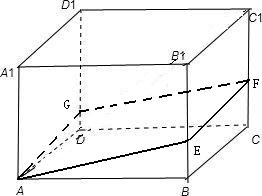
解答：
解；如图所示，
设过顶点A作正方体的截面AEFG与底面ABCD所成的角为θ，
则有：
=cosθ，
∴S截面AEFG=
＞1，
又当截面AEFG是正方体的对角面AB1C1D时，其面积最大，最大为
，
则截面面积的取值范围是 (1，
]．
故答案为：(1，
]．
解；如图所示，设过顶点A作正方体的截面AEFG与底面ABCD所成的角为θ，
则有：
| S 底面ABCD |
| S 截面AEFG |
∴S截面AEFG=
| S 底面ABCD |
| cosθ |
又当截面AEFG是正方体的对角面AB1C1D时，其面积最大，最大为
| 2 |
则截面面积的取值范围是 (1，
| 2 |
故答案为：(1，
| 2 |
点评：本小题主要考查棱柱的结构特征、正方体的结构特征的应用、正方体的截面等基础知识，考查空间想象能力．属于基础题．
练习册系列答案
优生乐园系列答案
相关题目
已知长方体ABCD-A1B1C1D1中，棱AB=BC=3，BB1=4，连接B1C，在CC1上有点E，使得A1C⊥平面EBD，BE交B1C于F．
在边长为a的正方体ABCD-A1B1C1D1中，E、F分别为AB与C1D1的中点．
（1）求证：四边形A1ECF是菱形；
（2）求证：EF⊥平面A1B1C；
（3）求A1B1与平面A1ECF所成角的正切值．
（1）求证：四边形A1ECF是菱形；
（2）求证：EF⊥平面A1B1C；
（3）求A1B1与平面A1ECF所成角的正切值．
如图，M，N，K分别是正方体ABCD-A1B1C1D1的棱AB，CD，C1D1的中点．
如图，已知长方体ABCD-A1B1C1D1，AB=BC=1，BB1=2，连接B1C，过B点作B1C．已知正四棱柱ABCD―A1B1C1D1中，AB=2，AA1=3.
（I）求证：A1C⊥BD；
（II）求直线A1C与侧面BB1C1C所成的角的正切值；
|