题目内容
18.若x>0,则函数y=x+$\frac{1}{2x+1}$的最小值为$\sqrt{2}-\frac{1}{2}$.分析 构造思想,函数y=x+$\frac{1}{2x+1}$变形为y=(x+$\frac{1}{2}$)+($\frac{\frac{1}{2}}{x+\frac{1}{2}}$)$-\frac{1}{2}$,利用基本不等式的性质即可得出.
解答 解:x>0,
函数y=x+$\frac{1}{2x+1}$=(x+$\frac{1}{2}$)+($\frac{\frac{1}{2}}{x+\frac{1}{2}}$)$-\frac{1}{2}$≥2$\sqrt{\frac{1}{2}}-\frac{1}{2}$=$\sqrt{2}-\frac{1}{2}$,当且仅当x=$\frac{\sqrt{2}-1}{2}$时取等号.
∴函数y=x+$\frac{1}{2x+1}$的最小值为$\sqrt{2}-\frac{1}{2}$.
故答案为:$\sqrt{2}-\frac{1}{2}$.
点评 本题考查了构造思想,基本不等式的性质的运用,属于基础题.

练习册系列答案
相关题目
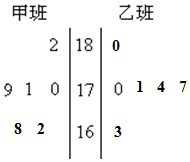 随机抽取某中学甲乙两班各6名学生,测量他们的身高(单位:cm),获得身高数据的茎叶图如图.
随机抽取某中学甲乙两班各6名学生,测量他们的身高(单位:cm),获得身高数据的茎叶图如图.