题目内容
6.已知{an}是公差不为零的等差数列,a1=1且a1,a3,a9,成等比数列.(1)求数列{an}的通项公式;
(2)求数列$\{{2^{a_n}}+{a_n}\}$的前n项和Sn.
分析 (1)设数列{an}的公差为d≠0.由a1=1,且a1,a3,a9成等比数列,可得a32=a1•a9,即(1+2d)2=1×(1+8d),解出d即可得出通项公式.
(2)根据等比数列和等差数列的前n项和公式,分组求和即可.
解答 解:(1):设数列{an}的公差为d≠0.
∵a1=1,且a1,a3,a9成等比数列,
∴a32=a1•a9,即(1+2d)2=1×(1+8d),
∴4d2=8d,
∵d≠0,∴d=1.
∴an=a1+(n-1)=1+n-1=n.
(Ⅱ)∵${2}^{{a}_{n}}$+an=2n+n,
∴数列$\{{2^{a_n}}+{a_n}\}$的前n项和Sn=$\frac{2(1-{2}^{n})}{1-2}$+$\frac{n(n+1)}{2}$=2n+1-2+$\frac{n(n+1)}{2}$
点评 本题考查等差数列的通项公式的运用以及前n项和公式,考查等比数列的中项的性质,考查运算能力,属于中档题

练习册系列答案
相关题目
3.设集合A={x|(x-1)(x-2)<0},集合B={x|1<x<3},则A∪B=( )
| A. | {x|-3<x<3} | B. | {x|1<x<2} | C. | {x|-1<x<1} | D. | {x|1<x<3} |
1.直线2x-2y+1=0的倾斜角是( )
| A. | 30° | B. | 45° | C. | 120° | D. | 135° |
15.已知f(x)=ax3+bx+2014x2017-4其中a,b为常数,若f(-2)=2,则f(2)=( )
| A. | -2 | B. | -4 | C. | -6 | D. | -10 |
16.已知集合M={x||x-1|<1},N={x|x2>4},则( )
| A. | M∩N=∅ | B. | M∩N=M | C. | M∩N=N | D. | M∪N=R |
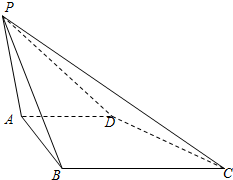 如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,AD∥BC,AB⊥BC,侧面PAD同时垂直侧面PAB与侧面PDC.若PA=AB=AD=$\frac{{\sqrt{3}}}{3}$PB,则$\frac{BC}{AD}$=$\frac{3}{2}$,直线PC与底面ABCD所成角的正切值为$\frac{\sqrt{6}}{6}$.
如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,AD∥BC,AB⊥BC,侧面PAD同时垂直侧面PAB与侧面PDC.若PA=AB=AD=$\frac{{\sqrt{3}}}{3}$PB,则$\frac{BC}{AD}$=$\frac{3}{2}$,直线PC与底面ABCD所成角的正切值为$\frac{\sqrt{6}}{6}$.