题目内容
11.为了活跃学生课余生活,我校高三年级部计划使用不超过1200元的资金购买单价分别为90元、120元的排球和篮球.根据需要,排球至少买3个,篮球至少买2个,并且排球的数量不得超过篮球数量的2倍,则能买排球和篮球的个数之和的最大值是12.分析 设买排球x个,篮球y个,由题意列关于x,y的不等式组,作出可行域,化目标函数为直线方程的斜截式,数形结合得到最优解,联立方程组求得最优解的坐标,代入目标函数得答案.
解答 解:设买排球x个,篮球y个,买排球和篮球的个数之和z=x+y.
则$\left\{\begin{array}{l}{x≥3}\\{y≥2}\\{x≤2y}\\{90x+120y≤1200}\end{array}\right.$,
由约束条件作出可行域如图: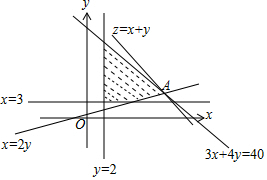
联立$\left\{\begin{array}{l}{x=2y}\\{3x+4y=40}\end{array}\right.$,解得A(8,4),
化目标函数z=x+y为y=-x+z,由图可知,
当直线y=-x+z过点A时,直线在y轴上的截距最大,z有最大值为12.
故答案为:12.
点评 本题考查简单的线性规划,考查了数形结合的解题思想方法,是中档题.

练习册系列答案
相关题目
1.已知f(x)=sin(ωx+θ),其中ω>0,θ∈(0,$\frac{π}{2}$),f(x1)=f(x2)=0,|x2-x1|min=$\frac{π}{2}$.f(x)=f($\frac{π}{3}-x$),将f(x)的图象向左平移$\frac{π}{6}$个单位得G(x),则G(x)的单调递减区间是( )
| A. | [kπ,kπ+$\frac{π}{2}$] | B. | [kπ+$\frac{π}{6}$,kπ+$\frac{2π}{3}$] | C. | [kπ+$\frac{π}{3}$,kπ+$\frac{5π}{6}$] | D. | [kπ+$\frac{π}{12}$,kπ+$\frac{7π}{12}$] |
2.命题“?x∈R,x2-x+1>0”的否定是( )
| A. | ?x∈R,x2-x+1≤0 | B. | ?x∈R,x2-x+1<0 | ||
| C. | ?x0∈R,x02-x0+1≤0 | D. | ?x0∈R,x02-x0+1<0 |
19.函数y=3sin(2x-$\frac{π}{3}$)的图象,经过下列哪个平移变换,可以得到函数y=3sin2x的图象( )
| A. | 向左平移$\frac{π}{6}$ | B. | 向右平移 $\frac{π}{6}$ | C. | 向左平移 $\frac{π}{3}$ | D. | 向右平移$\frac{π}{3}$ |
16.若复数z满足(2-i)z=1-i(i为虚数单位),则复数z在复平面内对应的点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
20.已知函数f(x)=cos(2x-φ)-$\sqrt{3}$sin(2x-φ)(|φ|<$\frac{π}{2}$)的图象向右平移$\frac{π}{12}$个单位后关于y轴对称,则f(x)在区间$[{-\frac{π}{2},0}]$上的最小值为( )
| A. | -1 | B. | $\sqrt{3}$ | C. | $-\sqrt{3}$ | D. | -2 |