题目内容
直线
x-y-3=0绕它与x轴的交点逆时针旋转
所得直线为（ ）
| 3 |
| π |
| 3 |
A、
| ||
B、
| ||
C、x-
| ||
D、x+
|
考点：直线的点斜式方程
专题：计算题
分析：设直线l倾斜角等于
，由题意可得所求直线的倾斜角等于
，可得所求直线的斜率，用点斜式求出直线方程．
| π |
| 3 |
| 2π |
| 3 |
解答：
解：直线
x-y-3=0的斜率等于
，设倾斜角等于
，
绕它与x轴的交点（
，0）逆时针旋转
，
所得到的直线的倾斜角等于
+
=
，
∴得到的直线的斜率为-
，
∴直线的方程为y=-
（x-
），即
x+y-3=0，
故选A．
| 3 |
| 3 |
| π |
| 3 |
绕它与x轴的交点（
| 3 |
| π |
| 3 |
所得到的直线的倾斜角等于
| π |
| 3 |
| π |
| 3 |
| 2π |
| 3 |
∴得到的直线的斜率为-
| 3 |
∴直线的方程为y=-
| 3 |
| 3 |
| 3 |
故选A．
点评：本题考查直线的倾斜角和斜率的关系，考查用点斜式求直线方程的方法，求出所求直线的斜率是解题的关键．
练习册系列答案
名校课堂系列答案
相关题目
设P是椭圆
+
=1上一点，F1、F2是椭圆的焦点，若|PF1|等于4，则|PF2|等于（ ）
| x2 |
| 169 |
| y2 |
| 144 |
| A、22 | B、21 | C、20 | D、13 |
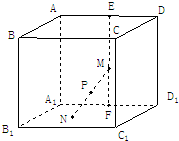如图，在棱长为4的正方体ABCD-A1B1C1D1中，E、F分别是AD，A1D1的中点，长为2的线段MN的一个端点M在线段EF上运动，另一个端点N在底面A1B1C1D1上运动，则线段MN的中点P在二面角A-A1D1-B1内运动所形成的轨迹（曲面）的面积为（ ）| A、4π | ||
| B、π | ||
C、
| ||
| D、2π |
在△ABC中，A=
，C=
，b=2，则此三角形的最小边长是（ ）
| π |
| 3 |
| π |
| 6 |
| A、1 | ||||
B、2
| ||||
C、
| ||||
D、
|