题目内容
1.已知⊙C1:(x+1)2+y2=1,⊙C2:(x-1)2+y2=r2(r>0),⊙C1内切⊙C2于点A,P是两圆公切线l上异于A的一点,直线PQ切⊙C1于点Q,PR切⊙C2于点R,且Q,R均不与A重合,直线C1Q,C2R相交于点M.(1)求M的轨迹C的方程;
(2)若直线MC1与x轴不垂直,它与C的另一个交点为N,M′是点M关于x轴的对称点,求证:直线NM′过定点.
分析 (1)由⊙C1内切⊙C2于点A,求出⊙C2的方程为(x-1)2+y2=9,由直线PQ切⊙C1于点Q,PR切⊙C2于点R,得到C1Q⊥PQ,C2R⊥PR,连结PM,推导出点M的轨迹C是以C1,C2为焦点,长轴长为4的椭圆(除去长轴端点),由此能求出M的轨迹C的方程.(2)设直线MN的方程为x=ty-1(t≠0),联立$\left\{\begin{array}{l}{x=ty-1}\\{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1}\end{array}\right.$,得:(3t2+4)y2-6ty-9=0,由此利用根的判别式、韦达定理、直线方程,结合已知条件,能证明直线NM′过定点(-4,0).
解答 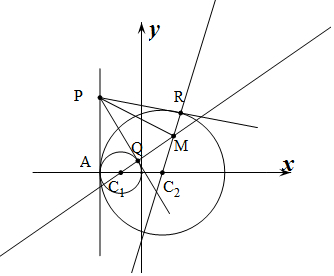 解:(1)∵⊙C1:(x+1)2+y2=1,⊙C2:(x-1)2+y2=r2(r>0),⊙C1内切⊙C2于点A,
解:(1)∵⊙C1:(x+1)2+y2=1,⊙C2:(x-1)2+y2=r2(r>0),⊙C1内切⊙C2于点A,
∴r-1=2,解得r=3,
∴⊙C2的方程为(x-1)2+y2=9,
∵直线PQ切⊙C1于点Q,PR切⊙C2于点R,
∴C1Q⊥PQ,C2R⊥PR,
连结PM,在Rt△PQM与Rt△PRM中,
|PQ|=|PA|=|PR|,|PM|=|PM|,
∴|QM|=|RM|,
∴|MC1|+|MC2|=|MQ|+|C1Q|=|MR|+|C1Q|+|C2M|=|C1Q|+|C2R|=4>2=|C1C2|,
∴点M的轨迹C是以C1,C2为焦点,长轴长为4的椭圆(除去长轴端点),
∴M的轨迹C的方程为$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}$=1(y≠0).
证明:(2)依题意,设直线MN的方程为x=ty-1(t≠0),M(x1,y1),N(x2,y2),
则M′(x1,-y1),且x1≠x2,y1+y2≠0,
联立$\left\{\begin{array}{l}{x=ty-1}\\{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1}\end{array}\right.$,消去x,并整理,得:(3t2+4)y2-6ty-9=0,
△=(-6t)2-4×(-9)(3t2+4)=144t2+144>0,
${y}_{1}+{y}_{2}=\frac{6t}{3{t}^{2}+4}$,${y}_{1}{y}_{2}=-\frac{9}{3{t}^{2}+4}$,
直线M′N的方程为y+y1=$\frac{{y}_{2}+{y}_{1}}{{x}_{2}-{x}_{1}}(x-{x}_{1})$,
令y=0,得:
x=$\frac{{y}_{1}({x}_{2}-{x}_{1})}{{y}_{2}+{y}_{1}}+{x}_{1}$=$\frac{{y}_{1}{x}_{2}+{x}_{1}{y}_{2}}{{y}_{2}+{y}_{1}}$
=$\frac{{y}_{1}(t{y}_{2}-1)+{y}_{2}(t{y}_{1}-1)}{{y}_{2}+{y}_{1}}$
=$\frac{2t{y}_{1}{y}_{2}}{{y}_{2}+{y}_{1}}-1$
=$\frac{\frac{-18t}{3{t}^{2}+4}}{\frac{6t}{3{t}^{2}+4}}$-1=-4.
∴直线NM′过定点(-4,0).
点评 本题考查点的轨迹方程的求法,考查直线过定点的证明,考查椭圆、根的判别式、韦达定理、直线方程等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、函数与方程思想,考查创新意识、应用意识,是中档题.

| A. | m=1或m=-2 | B. | m=1 | C. | m=-2 | D. | m的值不存在 |
| A. | 10 | B. | 5 | C. | -10 | D. | -5 |
 为了打好脱贫攻坚战,某贫困县农科院针对玉米种植情况进行调研,力争有效地改良玉米品种,为农民提供技术支援.现对已选出的一组玉米的茎高进行统计,获得茎叶图如图(单位:厘米),设茎高大于或等于180厘米的玉米为高茎玉米,否则为矮茎玉米.
为了打好脱贫攻坚战,某贫困县农科院针对玉米种植情况进行调研,力争有效地改良玉米品种,为农民提供技术支援.现对已选出的一组玉米的茎高进行统计,获得茎叶图如图(单位:厘米),设茎高大于或等于180厘米的玉米为高茎玉米,否则为矮茎玉米.(1)完成2×2列联表,并判断是否可以在犯错误概率不超过1%的前提下,认为抗倒伏与玉米矮茎有关?
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(2)为了改良玉米品种,现采用分层抽样的方法从抗倒伏的玉米中抽出5株,再从这5株玉米中选取2株进行杂交试验,选取的植株均为矮茎的概率是多少?
(Ⅰ)请完成如下列联表;
| 对服务好评 | 对服务不满意 | 合计 | |
| 对 商品 好评 | |||
| 对商品不满意 | |||
| 合 计 |
(Ⅲ)若针对商品的好评率,采用分层抽样的方式从这200次交易中取出5次交易,并从中选择两次交易进行客户回访,求只有一次好评的概率.
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |