Question

正三棱锥的高为1，底面边长为2，正三棱锥内有一个球与其四个面相切．则球的表面积为

 

．

Answer 1

考点：球的体积和表面积

专题：计算题,空间位置关系与距离

分析：设球的半径为r，以球心O为顶点，棱锥的四个面为底面把正三棱锥分割为四个小棱锥，求出r，由此能求出球的表面积．

解答： 解：如图，过点P作PD⊥平面ABC于D，
连结并延长AD交BC于E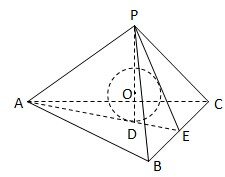，连结PE，△ABC是正三角形，
∴AE是BC边上的高和中线，D为△ABC的中心．
∵AB=2，
∴DE=

3

3

，
∵PD=1，
∴PE=

2 3

3

∴S_△PBC=

1

2

×2×

2 3

3

=

2 3

3

设球的半径为r，以球心O为顶点，
棱锥的四个面为底面把正三棱锥分割为四个小棱锥，
则

1

3

×

3

4

×4×1=

1

3

×(

3

4

×4+3×

2 3

3

)r，
∴r=

1

3

，
∴球的表面积为

4

9

π．
故答案为：

4

9

π．

点评：本题考查棱锥的全面积和体积的求法，考查球的表面积的求法，解题时要认真审题，注意空间思维能力的培养．