题目内容
已知直线l过点P(2,0),斜率为 直线l和抛物线y2=2x相交于A、B两点,设线段AB的中点为M,求:(1)|PM|; (2)|AB|.
直线l和抛物线y2=2x相交于A、B两点,设线段AB的中点为M,求:(1)|PM|; (2)|AB|.
 直线l和抛物线y2=2x相交于A、B两点,设线段AB的中点为M,求:(1)|PM|; (2)|AB|.
直线l和抛物线y2=2x相交于A、B两点,设线段AB的中点为M,求:(1)|PM|; (2)|AB|.(1) ;(2)
;(2)
 ;(2)
;(2)
试题分析:(1)写出过点P(2,0)的直线方程的参数方程,联立抛物线的方程得到一个含参数t二次方程.通过韦达定理即定点到中点的距离可得
 故填
故填 .
.(2)弦长公式|AB|=|t2-t1|再根据韦达定理可得
 故填
故填 .本题主要知识点是定点到弦所在线段中点的距离.弦长公式.这两个知识点都是参数方程中的长测知识点.特别是到中点的距离的计算要理解清楚.
.本题主要知识点是定点到弦所在线段中点的距离.弦长公式.这两个知识点都是参数方程中的长测知识点.特别是到中点的距离的计算要理解清楚.试题解析:(1)∵直线l过点P(2,0),斜率为

设直线的倾斜角为α,tanα=
 sinα=
sinα= cosα=
cosα=
∴直线l的参数方程为
 (t为参数)(*) 1分
(t为参数)(*) 1分∵直线l和抛物线相交,将直线的参数方程代入抛物线方程y2=2x中,整理得
8t2-15t-50=0,且Δ=152+4×8×50>0,
设这个一元二次方程的两个根为t1、t2,
由根与系数的关系,得t1+t2=
 t1t2=
t1t2= 3分
3分由M为线段AB的中点,根据t的几何意义,
得
 4分
4分(2)|AB|=|t2-t1|
=
 7分
7分
练习册系列答案
相关题目
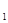 :
: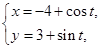 (t为参数), C
(t为参数), C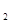 :
: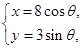 (
(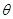 为参数)。
为参数)。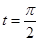 ,Q为C
,Q为C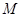 中点
中点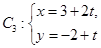 (t为参数)距离的最小值。
(t为参数)距离的最小值。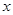 轴的正半轴为极轴建立极坐标系,已知曲线
轴的正半轴为极轴建立极坐标系,已知曲线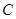 的极坐标方程为
的极坐标方程为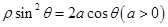 ,过点
,过点 的直线
的直线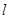 的参数方程为
的参数方程为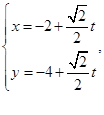 (
(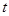 为参数),直线
为参数),直线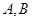 两点.
两点.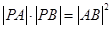 ,求
,求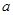 的值.
的值.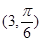 ,半径r=1.
,半径r=1. 与圆交于
与圆交于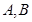 两点,求弦
两点,求弦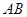 的长.
的长.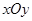 中,
中,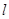 是过定点
是过定点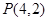 且倾斜角为
且倾斜角为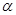 的直线;在极坐标系(以坐标原点
的直线;在极坐标系(以坐标原点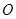 为极点,以
为极点,以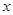 轴非负半轴为极轴,取相同单位长度)中,曲线
轴非负半轴为极轴,取相同单位长度)中,曲线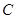 的极坐标方程为
的极坐标方程为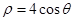 .
.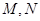 ,求
,求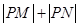 的取值范围.
的取值范围.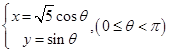 和
和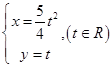 ,它们的交点坐标为____________
,它们的交点坐标为____________ 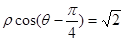 与圆
与圆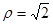 的公共点个数是________.
的公共点个数是________.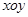 中,已知曲线
中,已知曲线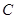 的参数方程是
的参数方程是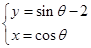 (
(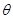 是参数),若以
是参数),若以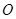 为极点,
为极点,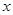 轴的正半轴为极轴,则曲线
轴的正半轴为极轴,则曲线
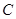 的参数方程为
的参数方程为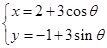 (
(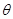 为参数),直线
为参数),直线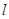 的方程为
的方程为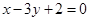 ,则曲线
,则曲线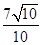 的点的个数为( )
的点的个数为( )