题目内容
学校体育场南侧有4个大门，北侧有3个大门，西侧有2个大门，某学生到该体育场训练，但必须是从南或北门进入，从西门或北门出去，则他进出门的方案有（ ）
| A、7个 | B、12个 |
| C、24个 | D、35个 |
考点：分步乘法计数原理,排列、组合的实际应用
专题：计算题,排列组合
分析：由题意，分两步完成，进入有7种方法，出去有5种方法，利用乘法原理可得结论．
解答：
解：由题意，分两步完成，进入有7种方法，出去有5种方法，利用乘法原理可得他进出门的方案有7×5=35种．
故选D．
故选D．
点评：本题考查计数原理的运用，考查学生分析解决问题的能力，属于基础题．
练习册系列答案
相关题目
b=0是函数f（x）=x2+bx+c为偶函数的（ ）条件．
| A、充分而不必要 |
| B、必要而不充分 |
| C、充分必要 |
| D、既不充分也不必要 |
运行如方框内的程序，若输入x=4，则输出的结果是（ ）| A、12 | B、3 | C、4 | D、5 |
已知集合A={x|4-x2＞0}，B={x|
＞0}，则A∩B等于（ ）
| x-1 |
| x |
| A、（-∞，0）∪（2，+∞） |
| B、（2，+∞） |
| C、（1，2） |
| D、（-2，0）∪（1，2） |
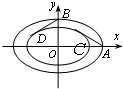简化北京奥动会主体育场“鸟巢”的钢结构俯视图如图所示，内外两圈的钢骨架是离心率相同的椭圆，外层椭圆顶点向内层椭圆引切线AC、BD，设内层椭圆方程为