题目内容
已知集合A={x|4-x2＞0}，B={x|
＞0}，则A∩B等于（ ）
| x-1 |
| x |
| A、（-∞，0）∪（2，+∞） |
| B、（2，+∞） |
| C、（1，2） |
| D、（-2，0）∪（1，2） |
考点：交集及其运算
专题：集合
分析：分别求解二次不等式和分式不等式化简集合A，B，然后直接利用交集运算求解．
解答：
解：由4-x2＞0，得x2＜4，-2＜x＜2．
∴A={x|4-x2＞0}={x|-2＜x＜2}，
由
＞0，得x（x-1）＞0，即x＜0或x＞1．
∴B={x|
＞0}={x|x＜0或x＞1}，
则如图，
A∩B=（-2，0）∪（1，2）．
故选：D．
∴A={x|4-x2＞0}={x|-2＜x＜2}，
由
| x-1 |
| x |
∴B={x|
| x-1 |
| x |
则如图，
A∩B=（-2，0）∪（1，2）．
故选：D．
点评：本题考查了交集及其运算，考查了不等式的解法，是基础题．
练习册系列答案
相关题目
已知角θ为第四象限角，且tanθ=-
，则sinθ+cosθ=（ ）
| 3 |
| 4 |
A、
| ||
B、
| ||
C、-
| ||
D、-
|
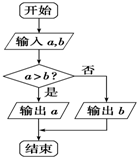如图所示的程序框图，其功能是（ ）| A、输入a，b的值，按从小到大的顺序输出它们的值 |
| B、输入a，b的值，按从大到小的顺序输出它们的值 |
| C、求a，b的最大值 |
| D、求a，b的最小值 |
数列0.9，0.99，0.999，0.9999，…的一个通项公式是（ ）
A、an=1-
| ||
B、an=1-
| ||
C、an=1-
| ||
D、an=1-
|
已知α，β均为锐角，且3sinα=2sinβ，3cosα+2cosβ=3，则α+2β的值为（ ）
A、
| ||
B、
| ||
C、
| ||
| D、π |
若函数f（x）可导，则f′（x0）等于（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
学校体育场南侧有4个大门，北侧有3个大门，西侧有2个大门，某学生到该体育场训练，但必须是从南或北门进入，从西门或北门出去，则他进出门的方案有（ ）
| A、7个 | B、12个 |
| C、24个 | D、35个 |