题目内容
20.直线(m+3)x+my-6=0过定点(2,-2),它与圆x2-4x+y2-1=0的位置关是相交.(填:相交、相切、相离或不确定)分析 把直线方程化为m(x+y)+(3x-6)=0,令$\left\{\begin{array}{l}{x+y=0}\\{3x-6=0}\end{array}\right.$,求出方程组的解即可,确定定点在圆内,即可得出结论.
解答 解:直线(m+3)x+my-6=0可化为m(x+y)+(3x-6)=0,
令$\left\{\begin{array}{l}{x+y=0}\\{3x-6=0}\end{array}\right.$,
解得x=2,y=-2,
所以该直线过定点(2,-2),
因为22-4×2+(-2)2-1=-1<0
所以直线与圆相交
故答案为:(2,-2),相交
点评 本题考查了直线恒过定点问题,解题的关键是将方程中的参数分离,建立方程组求出点的坐标.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
10.已知某几何体的三视图的侧视图是一个正三角形,如图所示,则该几何体的体积等于( )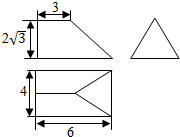

| A. | 12$\sqrt{3}$ | B. | 16$\sqrt{3}$ | C. | 20$\sqrt{3}$ | D. | 32$\sqrt{3}$ |
15.已知过点C(6,-8)作圆x2+y2=25的切线,切点分别为A,B,那么点C到直线AB的距离为( )
| A. | 15 | B. | 10 | C. | $\frac{15}{2}$ | D. | 5 |
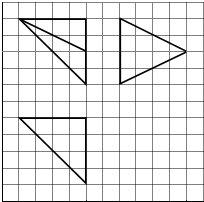 如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的各个面中,直角三角形的个数是( )
如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的各个面中,直角三角形的个数是( )