题目内容
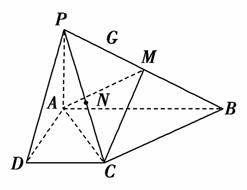
(2013·长春三校调研)如图,已知四棱锥P-ABCD的底面为直角梯形,AB∥CD,∠DAB=90°,PA⊥底面ABCD,且PA=AD=DC=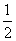 AB=1,M是PB的中点.
AB=1,M是PB的中点.
(1)求证:AM=CM;
(2)若N是PC的中点,求证:DN∥平面AMC.
 [
[
解析] (1)在直角梯形ABCD中,AD=DC=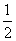 AB=1,
AB=1,
∴AC=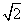 ,BC=
,BC=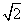 ,∴BC⊥AC,
,∴BC⊥AC,
又PA⊥平面ABCD,BC⊂平面ABCD,∴BC⊥PA,
又PA∩AC=A,∴BC⊥平面PAC,
∴BC⊥PC.
在Rt△PAB中,M为PB的中点,则AM=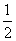 PB,
PB,
在Rt△PBC中,M为PB的中点,则CM=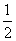 PB,
PB,
∴AM=CM.
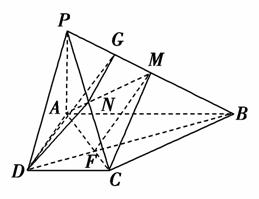
(2)如图,连接DB交AC于点F,
∵DC綊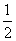 AB,∴DF=
AB,∴DF=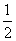 FB.
FB.
取PM的中点G,连接DG,FM,则DG∥FM,
又DG⊄平面AMC,FM⊂平面AMC,
∴DG∥平面AMC.
连接GN,则GN∥MC,∴GN∥平面AMC,
又GN∩DG=G,∴平面DNG∥平面AMC,
又DN⊂平面DNG,∴DN∥平面AMC.

练习册系列答案
相关题目
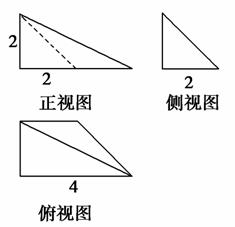
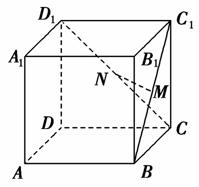

 Sh,其中S为底面面积,h为高).
Sh,其中S为底面面积,h为高).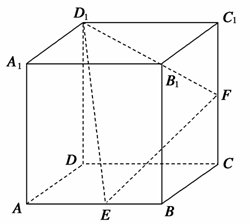
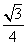 B.
B.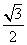
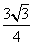 D.
D.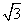
 B.1
B.1