题目内容
设F1、F2是椭圆E：
+
=1（a＞b＞0）的左右焦点，P是直线x=
a上一点，△F2PF1是底角为30°的等腰三角形，则椭圆E的离心率为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| 4 |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点：椭圆的简单性质
专题：计算题,圆锥曲线的定义、性质与方程
分析：利用△F2PF1是底角为30°的等腰三角形，可得|PF2|=|F2F1|，根据P为直线x=
a上一点，可建立方程，由此可求椭圆的离心率．
| 4 |
| 3 |
解答：
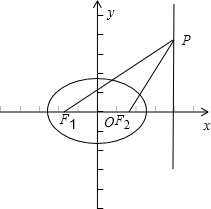解：∵△F2PF1是底角为30°的等腰三角形，
∴|PF2|=|F2F1|
∵P为直线x=
a上一点
∴2（
a-c）=2c
∴e=
=
故选：B．
解：∵△F2PF1是底角为30°的等腰三角形，∴|PF2|=|F2F1|
∵P为直线x=
| 4 |
| 3 |
∴2（
| 4 |
| 3 |
∴e=
| c |
| a |
| 2 |
| 3 |
故选：B．
点评：本题考查椭圆的几何性质，解题的关键是确定几何量之间的关系，属于基础题．
练习册系列答案
相关题目
PM2.5是指大气中直径小于或等于2.5微米的颗粒物，也称为可A肺颗粒物，般情况下PM2.5浓度越大，大气环境质量越差，茎叶图表示的是成都市区甲、乙两个监测站某10日内每天的PM2.5浓度读数（单位：μg/m3）则下列说法正确的是（ ）| A、这l0日内甲、乙监测站读数的极差相等 |
| B、这10日内甲、乙监测站读数的中位数中，乙的较大 |
| C、这10日内乙监测站读数的众数与中位数相等 |
| D、这10日内甲、乙监测站读数的平均数相等 |
已知f（n）=1+
+
+…+
（n∈N*），计算得f（2）=
，f（4）＞2，f（8）＞
，f（16）＞3，f（32）＞
，由此推算：当n≥2时，有（ ）
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
| 3 |
| 2 |
| 5 |
| 2 |
| 7 |
| 2 |
A、f（2n）＞
| ||
B、f（2n）＞
| ||
C、f（2n）＞
| ||
D、f（2n）＞
|
执行如图所示的程序框图，若输出k=2，则输入x的取值范围是（ ）
| A、（28，57] |
| B、[28，57） |
| C、（28，57） |
| D、[28，57] |
已知变量x，y满足
，则x+2y的最小值是（ ）
|
| A、6 | B、5 | C、3 | D、2 |
等差数列{an}，a7-2a4=-1，且a3=0，则公差d=（ ）
| A、-2 | ||
B、-
| ||
C、
| ||
| D、2 |
f（x）=ln（4+3x-x2）的单调递增区间是（ ）
A、（-∞，
| ||
B、[
| ||
C、（-1，
| ||
D、[
|
如图，△ABC的AB边长为2，P，Q分别是AC，BC中点，记| AB |
| AP |
| BA |
| BQ |
| AB |
| AQ |
| BA |
| BP |
| A、m=2，n=4 |
| B、m=3，n=1 |
| C、m=2，n=6 |
| D、m=3n，但m，n的值不确定 |