题目内容
数列{an}满足：a1=2，an+1=an+2（n∈N*），则其前10项的和S10=（ ）
| A、100 | B、101 |
| C、110 | D、111 |
考点：数列递推式
专题：等差数列与等比数列
分析：由已知条件推导出数列{an}是首项为2，公差为2的等差数列，由此能求出其前10项的和S10．
解答：
解：∵数列{an}满足：a1=2，an+1=an+2（n∈N*），
∴数列{an}是首项为2，公差为2的等差数列，
∴其前10项的和S10=10×2+
×2=110．
故选：C．
∴数列{an}是首项为2，公差为2的等差数列，
∴其前10项的和S10=10×2+
| 10×9 |
| 2 |
故选：C．
点评：本题考查数列的前10项和的求法，是基础题，解题时要认真审题，注意等差数列的性质的灵活运用．
练习册系列答案
名师伴你成长课时同步学练测系列答案
相关题目
定义某种运算?，S=a?b的运算原理如图所示．设f（x）=（0?x）x-（3?x）．则f（3）=△ABC所在平面α外一点P到三角形三顶点的距离相等，那么点P在α内的射影一定是△ABC的（ ）
| A、外心 | B、内心 |
| C、重心 | D、以上都不对 |
将两个数a=2，b=-1交换，使a=-1，b=2，下列语句正确的是（ ）
A、 |
B、 |
C、 |
D、 |
如图，9名战士站成3行3列，现从这9名战士中随机选出2名战士分别担任正、副组长，要求这2名战士来自不同行且不同列，共有多少种不同的选法（ ）| A、18 | B、36 | C、72 | D、144 |
设函数f（x）=x+sinπx，则f（
）+f（
）+…+f（
）+f（
）的值为（ ）
| 1 |
| 2014 |
| 2 |
| 2014 |
| 4026 |
| 2014 |
| 4027 |
| 2014 |
| A、4027 | B、2014 |
| C、2013 | D、0 |
已知函数f（x）=sin（x-
）（x∈R），下面结论错误的是（ ）
| π |
| 2 |
| A、函数f（x）的最小正周期为2π | ||
B、函数f（x）在区间[0，
| ||
| C、函数f（x）的图象关于直线x=0对称 | ||
| D、函数f（x）的图象关于原点对称 |
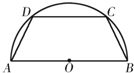如图，半径为2的半圆有一内接梯形ABCD，它的下底AB是⊙O的直径，上底CD的端点在圆周上．若双曲线以A，B为焦点，且过C，D两点，则当梯形ABCD的周长最大时，双曲线的实轴长为（ ）A、
| ||
B、2
| ||
C、
| ||
D、2
|
离散型随机变量的分布列为：
则x的值为（ ）
| ξ | 0 | 1 | 2 | 3 | ||||||
| P |
|
|
|
x |
A、
| ||
B、
| ||
C、
| ||
D、
|