题目内容
某堂训练课上,一射击运动员对同一目标独立地进行了四次射击,已知他至少命中一次的概率为
,则四次射击中,他命中2次的概率为( )
| 65 |
| 81 |
A、
| ||
B、
| ||
C、
| ||
| D、以上都不对 |
考点:n次独立重复试验中恰好发生k次的概率
专题:计算题,概率与统计
分析:利用此射手至少命中一次的概率为
,求出每次射击命中的概率,再求出四次射击中,他命中2次的概率
| 65 |
| 81 |
解答:
解:由题意可知一射手对同一目标独立地射击四次全都没有命中的概率为1-
=
.
设此射手每次射击命中的概率为p,则(1-p)4=
,∴p=
.
∴四次射击中,他命中2次的概率为
•(
)2•(
)2=
.
故选:C.
| 65 |
| 81 |
| 16 |
| 81 |
设此射手每次射击命中的概率为p,则(1-p)4=
| 16 |
| 81 |
| 1 |
| 3 |
∴四次射击中,他命中2次的概率为
| C | 2 4 |
| 1 |
| 3 |
| 2 |
| 3 |
| 8 |
| 27 |
故选:C.
点评:本题考查n次独立重复试验中恰好发生k次的概率,确定此射手每次射击命中的概率是关键.

练习册系列答案
相关题目
在复数范围内,方程x2=-1的解是( )
| A、±1 | B、-1 | C、±i | D、i |
设函数f(x)=x+sinπx,则f(
)+f(
)+…+f(
)+f(
)的值为( )
| 1 |
| 2014 |
| 2 |
| 2014 |
| 4026 |
| 2014 |
| 4027 |
| 2014 |
| A、4027 | B、2014 |
| C、2013 | D、0 |
把黑、红、白3张纸牌分给甲、乙、丙三人,每人一张,则事件“甲分得红牌”与“乙分得红牌”是( )
| A、对立事件 |
| B、必然事件 |
| C、不可能事件 |
| D、互斥但不对立事件 |
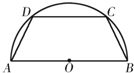 如图,半径为2的半圆有一内接梯形ABCD,它的下底AB是⊙O的直径,上底CD的端点在圆周上.若双曲线以A,B为焦点,且过C,D两点,则当梯形ABCD的周长最大时,双曲线的实轴长为( )
如图,半径为2的半圆有一内接梯形ABCD,它的下底AB是⊙O的直径,上底CD的端点在圆周上.若双曲线以A,B为焦点,且过C,D两点,则当梯形ABCD的周长最大时,双曲线的实轴长为( )A、
| ||
B、2
| ||
C、
| ||
D、2
|
如图是“集合”的知识结构图,如果要加入“子集”,则应放在( )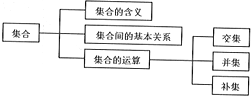

| A、“集合的含义”的下位 |
| B、“集合间的基本关系”的下位 |
| C、“交集”的下位 |
| D、“集合的运算”的下位 |
若数列{an}的前n项和Sn=n2-1,则a4=( )
| A、7 | B、8 | C、9 | D、17 |
吉安市高二数学竞赛中有一道难题,在30分钟内,学生甲内解决它的概率为
,学生乙能解决它的概率为
,两人在30分钟内独立解决该题,该题得到解决的概率为( )
| 1 |
| 5 |
| 1 |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|