题目内容
已知过点A(1,0)且斜率为k的直线l与圆C:(x-3)2+(y-2)2=1相交于P、Q两点,则AP•AQ的值为 .
考点:直线与圆相交的性质
专题:直线与圆
分析:根据切线长定理即可得到结论.
解答:
解: 圆心C(3,2),半径R=1,
圆心C(3,2),半径R=1,
设切线交圆于B,
则由切线长定理得AP•AQ=AB2,
∵AB=
=
=
=
,
∴AP•AQ=AB2=7,
故答案为:7
 圆心C(3,2),半径R=1,
圆心C(3,2),半径R=1,设切线交圆于B,
则由切线长定理得AP•AQ=AB2,
∵AB=
| AC2-BC2 |
| (3-1)2+22-1 |
| 4+4-1 |
| 7 |
∴AP•AQ=AB2=7,
故答案为:7
点评:本题主要考查直线和圆的位置关系的应用,根据切弦长定理是解决本题的关键.

练习册系列答案
相关题目
已知函数f(x)对于任意的x∈R都有f(x)<f(x+1),则f(x)在R上( )
| A、是单调增函数 |
| B、没有单调减区间 |
| C、可能存在单调增区间,也可能不存在单调增区间 |
| D、没有单调增区间 |
如果|
|=|
|=1,
与
的夹角为θ,
•
=
,则θ=( )
| a |
| b |
| a |
| b |
| a |
| b |
| 1 |
| 2 |
| A、90° | B、30° |
| C、60° | D、120° |
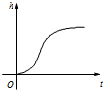
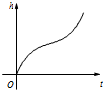
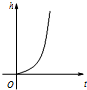
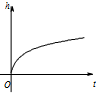
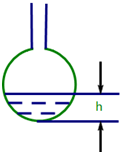 匀速地向下部是球形、上部是圆柱形的容器(如图所示)内注水,那么注水时间t与容器内水的高度h之间的函数关系 h=f(t)的图象大致是下图中的( )
匀速地向下部是球形、上部是圆柱形的容器(如图所示)内注水,那么注水时间t与容器内水的高度h之间的函数关系 h=f(t)的图象大致是下图中的( )