题目内容
16.设$\overrightarrow{{e}_{1}}$,$\overrightarrow{{e}_{2}}$为单位向量,且$\overrightarrow{{e}_{1}}$,$\overrightarrow{{e}_{2}}$的夹角为$\frac{π}{3}$,则向量$\overrightarrow{{e}_{1}}$在$\overrightarrow{{e}_{2}}$方向上的射影为$\frac{1}{2}$.分析 由已知可得,$|\overrightarrow{{e}_{1}}|=1$,结合$\overrightarrow{{e}_{1}}$,$\overrightarrow{{e}_{2}}$的夹角为$\frac{π}{3}$,代入向量在向量方向上的投影公式得答案.
解答 解:由题意可得:$|\overrightarrow{{e}_{1}}|=|\overrightarrow{{e}_{2}}|=1$,又$\overrightarrow{{e}_{1}}$,$\overrightarrow{{e}_{2}}$的夹角为$\frac{π}{3}$,
∴向量$\overrightarrow{{e}_{1}}$在$\overrightarrow{{e}_{2}}$方向上的射影为:$\frac{\overrightarrow{{e}_{1}}•\overrightarrow{{e}_{2}}}{|\overrightarrow{{e}_{2}}|}$=$|\overrightarrow{{e}_{1}}|$cos$\frac{π}{3}$=$\frac{1}{2}$.
故答案为:$\frac{1}{2}$.
点评 本题考查平面向量的数量积运算,考查了向量在向量方向上的投影,是基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.已知全集U={1,2,3,4,5},集合M={3,4,5},N={1,2,5},则集合(∁UM)∩N可以表示为( )
| A. | {1} | B. | {1,2} | C. | {1,2,3} | D. | {1,2,3,4} |
11.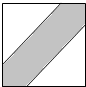 如图,在边长为25cm的正方形中挖去边长为23cm的两个等腰直角三角形,现有均匀的粒子散落在正方形中,问粒子落在中间阴影区域的概率是( )
如图,在边长为25cm的正方形中挖去边长为23cm的两个等腰直角三角形,现有均匀的粒子散落在正方形中,问粒子落在中间阴影区域的概率是( )
 如图,在边长为25cm的正方形中挖去边长为23cm的两个等腰直角三角形,现有均匀的粒子散落在正方形中,问粒子落在中间阴影区域的概率是( )
如图,在边长为25cm的正方形中挖去边长为23cm的两个等腰直角三角形,现有均匀的粒子散落在正方形中,问粒子落在中间阴影区域的概率是( )| A. | $\frac{529}{625}$ | B. | $\frac{96}{625}$ | C. | $\frac{23}{25}$ | D. | $\frac{2}{25}$ |
1.下列函数中值域为[0,+∞)的是( )
| A. | y=3x | B. | y=|x| | C. | y=x2-6x+7 | D. | $y=\frac{8}{x}$ |