题目内容
已知F1,F1是双曲线C1
-
=1(a>0,b>0)与椭圆C2:
+
=1的公共焦点,A,B是两曲线分别在第一,三象限的交点,且以F1,F2,A,B为顶点的四边形的面积为6
,则双曲线C1的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
| x2 |
| 25 |
| y2 |
| 9 |
| 6 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:双曲线的简单性质,椭圆的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:求出椭圆的焦点,利用以F1、F2、A、B为顶点的四边形的面积为6
,求出A的坐标,利用双曲线的定义求出a,即可求出双曲线的离心率.
| 6 |
解答:
解:椭圆C2:
+
=1的焦点坐标为(±4,0),
设A的坐标为(x,y)(x>0,y>0),则
∵以F1、F2、A、B为顶点的四边形的面积为6
,
∴2×
×8×y=6
,
∴y=
,
代入椭圆方程可得x=
,
∴|AF1|-|AF2|=2
,
∴e=
=
.
故选:A.
| x2 |
| 25 |
| y2 |
| 9 |
设A的坐标为(x,y)(x>0,y>0),则
∵以F1、F2、A、B为顶点的四边形的面积为6
| 6 |
∴2×
| 1 |
| 2 |
| 6 |
∴y=
3
| ||
| 4 |
代入椭圆方程可得x=
5
| ||
| 4 |
∴|AF1|-|AF2|=2
| 10 |
∴e=
| c |
| a |
2
| ||
| 5 |
故选:A.
点评:本题考查椭圆、双曲线的性质,考查三角形面积的计算,考查学生的计算能力,比较基础.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
已知cosα=
,α∈(-
,0),则sin2α的值为( )
| 3 |
| 4 |
| π |
| 2 |
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
函数f(x)=
的单调递增区间为( )
| lnx |
| x |
| A、(-∞,0)和(0,e) |
| B、(-∞,0)和(e,+∞) |
| C、(0,e) |
| D、(e,+∞) |
李华通过英语听力测试的概率是
,他连续测试5次,那么其中恰有2次获得通过的概率是( )
| 1 |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
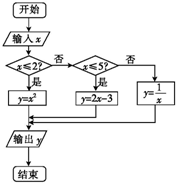 如图所示的程序框图,其作用是输入x的值,输出相应的y的值.
如图所示的程序框图,其作用是输入x的值,输出相应的y的值.