题目内容
已知log
(x+y+4)<log
(3x+y-2),若x-y<λ恒成立,则λ的取值范围是 .
| 1 |
| 2 |
| 1 |
| 2 |
考点:函数恒成立问题
专题:
分析:由对数不等式得到约束条件,作出可行域,求出使z=x-y取得最大值时的最优解,求出最大值,则λ的取值范围可求.
解答:
解:由log
(x+y+4)<log
(3x+y-2),得
,即
.
作出可行域如图,
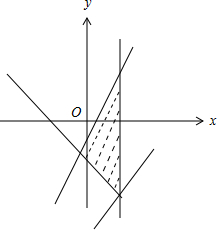
令z=x-y,则使目标函数取得最大值的最优解为B(3,-7),
此时z的最大值为10.
∴x-y<λ恒成立的λ的取值范围是[10,+∞).
故答案为:[10,+∞).
| 1 |
| 2 |
| 1 |
| 2 |
|
|
作出可行域如图,

令z=x-y,则使目标函数取得最大值的最优解为B(3,-7),
此时z的最大值为10.
∴x-y<λ恒成立的λ的取值范围是[10,+∞).
故答案为:[10,+∞).
点评:本题考查了函数恒成立问题,训练了数学转化思想方法,关键是化为线性规划知识求解,是中档题.

练习册系列答案
相关题目
设F1,F2分别是椭圆
+
=1(a>b>0)的左右焦点,若在其右准线上存在点P,使△PF1F2为等腰三角形,则椭圆的离心率的取值范围是( )
| x2 |
| a2 |
| y2 |
| b2 |
A、(0,
| ||||
B、(0,
| ||||
C、(
| ||||
D、(
|