题目内容
18.某家庭打算在2022年的年底花a万元购一套商品房,为此,计划从2016年初开始,每年年初存入一笔购房专用存款,使这笔款到2022年底连本带息共同a万元,如果每年的存款数额相同,依年利息p并按复利计算,则每年应存入x=$\frac{a}{{(1+p)}^{6}}$万元.分析 根据增长率,设出每年应存入x万元,得到关于x的方程,解出即可得到结论.
解答 解:设每年应存入x万元,
则x(1+p)6=a,
故x=$\frac{a}{{(1+p)}^{6}}$,
故答案为:x=$\frac{a}{{(1+p)}^{6}}$.
点评 本题考查指数函数的运用,考查学生分析解决问题的能力,属于基础题.

练习册系列答案
相关题目
9.等腰直角三角形ABC中,A=90°,A,B在双曲线E的同一支上,且线段AB通过双曲线的一个焦点,C为双曲线E的另一个焦点,则该双曲线的离心率为( )
| A. | $\sqrt{4-2\sqrt{2}}$ | B. | $\sqrt{5-2\sqrt{2}}$ | C. | $\sqrt{4+2\sqrt{2}}$ | D. | $\sqrt{5+2\sqrt{2}}$ |
13.按如图所示的程序框图运行后,输出的结果是63,则判断框中的整数M的值是( )
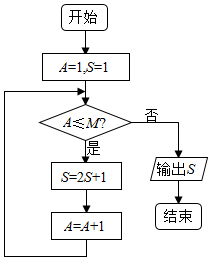

| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
10.执行如图所示的程序框图,若输入x=1,则输出y的值是( )
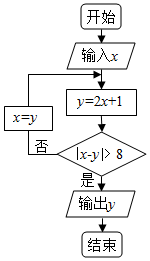

| A. | 7 | B. | 15 | C. | 23 | D. | 31 |
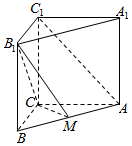 如图,直三棱柱ABC-A1B1C1中,AC=4,BC=3,AA1=4,AC⊥BC,点M在线段AB上.
如图,直三棱柱ABC-A1B1C1中,AC=4,BC=3,AA1=4,AC⊥BC,点M在线段AB上.
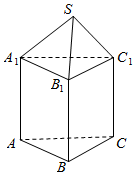 如图所示的几何体是由一个正三棱锥S-A1B1C1和一个所有棱长都相等的正三棱柱ABC-A1B1C1组合而成,且该几何体的外接球(几何体的所有顶点都在该球面上)的表面积为7π,则三棱锥S-A1B1C1的体积为$\frac{\sqrt{21}-3}{8}$.
如图所示的几何体是由一个正三棱锥S-A1B1C1和一个所有棱长都相等的正三棱柱ABC-A1B1C1组合而成,且该几何体的外接球(几何体的所有顶点都在该球面上)的表面积为7π,则三棱锥S-A1B1C1的体积为$\frac{\sqrt{21}-3}{8}$.