题目内容
若a,b,c为不全相等的正数,求证:lg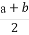 +lg
+lg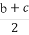 +lg
+lg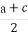 >lga+lgb+lgc.
>lga+lgb+lgc.
见解析
【解析】证明:由a,b,c为正数,得lg ≥lg
≥lg ;lg
;lg ≥lg
≥lg ;lg
;lg ≥lg
≥lg .
.
而a,b,c不全相等,
所以lg +lg
+lg +lg
+lg >lg
>lg +lg
+lg +lg
+lg =lg (abc)=lga+lgb+lgc.
=lg (abc)=lga+lgb+lgc.
即lg +lg
+lg +lg
+lg >lga+lgb+lgc.
>lga+lgb+lgc.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
题目内容
若a,b,c为不全相等的正数,求证:lg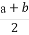 +lg
+lg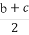 +lg
+lg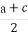 >lga+lgb+lgc.
>lga+lgb+lgc.
见解析
【解析】证明:由a,b,c为正数,得lg ≥lg
≥lg ;lg
;lg ≥lg
≥lg ;lg
;lg ≥lg
≥lg .
.
而a,b,c不全相等,
所以lg +lg
+lg +lg
+lg >lg
>lg +lg
+lg +lg
+lg =lg (abc)=lga+lgb+lgc.
=lg (abc)=lga+lgb+lgc.
即lg +lg
+lg +lg
+lg >lga+lgb+lgc.
>lga+lgb+lgc.

 阅读快车系列答案
阅读快车系列答案