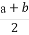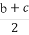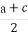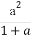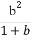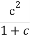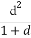题目内容
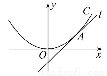
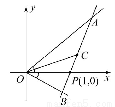
如图,射线OA,OB分别与x轴正半轴成45°和30°角,过点P(1,0)作直线AB分别交OA,OB于A,B两点,当AB的中点C恰好落在直线y=
x上时,求直线AB的方程.
(3+
)x-2y-3-=0
【解析】由题意可得kOA=tan 45°=1,
kOB=tan(180°-30°)=-
,
所以直线lOA:y=x,lOB:y=-x.
设A(m,m),B(-n,n),
所以AB的中点C(
,
).
由点C在直线y=
x上,且A,P,B三点共线得
解得m=,
所以A(,).
又P(1,0),所以kAB=kAP=
=
,
所以lAB: y=(x-1),
即直线AB的方程为(3+)x-2y-3-=0.
练习册系列答案
小学课时作业全通练案系列答案
相关题目
在样本的频率分布直方图中,共有11个小长方形,若中间一个小长方形的面积等于其他10个小长方形的面积和的
,且样本容量为160,则中间一组的频数为( )
(A)32 (B)0.2 (C)40 (D)0.25
某企业三月中旬生产A,B,C三种产品共3000件,根据分层抽样的结果,企业统计员制作了如下的统计表格:
产品类别 | A | B | C |
产品数量(件) |
| 1 300 |
|
样本容量 |
| 130 |
|
由于不小心,表格中A,C产品的有关数据已被污染看不清楚了,统计员只记得A产品的样本容量比C产品的样本容量多10,根据以上信息,可得C产品的数量是_________件.
