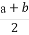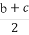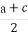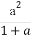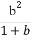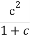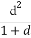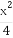题目内容
已知a,b为正数,求证:
(1)若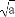
+1>
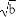,则对于任何大于1的正数x,恒有ax+
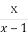>b成立.
(2)若对于任何大于1的实数x,恒有ax+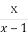>b成立,则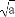+1>.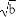
见解析
【解析】证明：(1)∵x>1,∴ax+
=a(x-1)+
+1+a≥2
+1+a=(+1)2.
∵+1>
(b>0),
∴(+1)2>b.
即ax+>b.
(2)∵ax+>b对于大于1的实数x恒成立,
即x>1时,[ax+]min>b,
而ax+=a(x-1)++1+a≥2+1+a=(+1)2,
当且仅当a(x-1)=,
即x=1+
>1时取等号.
故[ax+]min=(+1)2.
则(+1)2>b,即+1>.
练习册系列答案
相关题目
某企业三月中旬生产A,B,C三种产品共3000件,根据分层抽样的结果,企业统计员制作了如下的统计表格:
产品类别 | A | B | C |
产品数量(件) |
| 1 300 |
|
样本容量 |
| 130 |
|
由于不小心,表格中A,C产品的有关数据已被污染看不清楚了,统计员只记得A产品的样本容量比C产品的样本容量多10,根据以上信息,可得C产品的数量是_________件.
