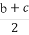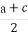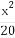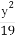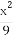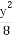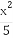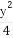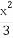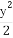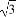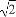题目内容
已知正数x,y,z满足5x+4y+3z=10.
(1)求证: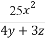
+
+
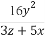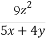≥5.
(2)求
+
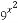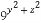的最小值.
(1)见解析 (2) 18
【解析】(1)根据柯西不等式,得
[(4y+3z)+(3z+5x)+(5x+4y)](
+
+
)≥(5x+4y+3z)2,
当且仅当
=
=
,
即x=
,y=
,z=
时取等号.
因为5x+4y+3z=10,
所以++≥
=5.
(2)根据平均值不等式,得
+
≥2
=2·
,
当且仅当x2=y2+z2时,等号成立.
根据柯西不等式,得
(x2+y2+z2)(52+42+32)≥(5x+4y+3z)2=100,
即x2+y2+z2≥2,当且仅当
=
=
时,
等号成立.
综上,+≥2·32=18.
当且仅当x=1,y=
,z=
时,等号成立.
所以+的最小值为18.
练习册系列答案
发散思维新课堂系列答案
相关题目
