题目内容
1.已知函数f(x)=x3+ax2+bx+c,x∈[-2,2]表示过原点的曲线,且在x=±1处的切线的倾斜角均为$\frac{3}{4}π$,有以下命题:①f(x)的解析式为f(x)=x3-4x,x∈[-2,2].
②f(x)的极值点有且只有一个.
③f(x)的最大值与最小值之和等于零.
其中正确命题的序号为①③.
分析 求出函数f(x)的导数,得到关于a,b,c的方程组,解出a,b,c的值,从而求出函数f(x)的单调区间,求出函数f(x)的最小值和最大值即可得到答案.
解答 解:f′(x)=3x2+2ax+b,
由题意得f(0)=0,f′(-1)=f′(1)=tan $\frac{3π}{4}$=-1.
∴$\left\{\begin{array}{l}{c=0}\\{3-2a+b=-1}\\{3+2a+b=-1}\end{array}\right.$,∴a=0,b=-4,c=0.
∴f(x)=x3-4x,x∈.故①正确.
由f′(x)=3x2-4=0得x1=-$\frac{2\sqrt{3}}{3}$,x2=$\frac{2\sqrt{3}}{3}$.
根据x1,x2分析f′(x)的符号、f(x)的单调性和极值点.
| x | -2 | (-2,-$\frac{2\sqrt{3}}{3}$) | -$\frac{2\sqrt{3}}{3}$ | (-$\frac{2\sqrt{3}}{3}$,$\frac{2\sqrt{3}}{3}$) | $\frac{2\sqrt{3}}{3}$ | ($\frac{2\sqrt{3}}{3}$,2) | 2 |
| f′(x) | + | 0 | - | 0 | + | ||
| f(x) | 0 | ↗ | $\frac{16\sqrt{3}}{9}$ | ↘ | $\frac{-16\sqrt{3}}{9}$ | ↗ | 0 |
f(x)min+f(x)max=0.
∴②错,③正确;
故答案为:①③.
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及切线问题,是一道中档题.

练习册系列答案
相关题目
11.已知向量$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为30°,且|$\overrightarrow{a}$|=$\sqrt{3}$,|$\overrightarrow{b}$|=2,则$\overrightarrow{a}$•$\overrightarrow{b}$等于( )
| A. | $2\sqrt{3}$ | B. | 3 | C. | $\sqrt{6}$ | D. | $\sqrt{3}$ |
16.已知数列{an}满足:a1=2,an+1=1-$\frac{1}{{a}_{n}}$,则a2016=( )
| A. | 2 | B. | $\frac{1}{2}$ | C. | -1 | D. | 1 |
6.某程序框图如图所示,若该程序运行后输出的值是10,则a的值是( )
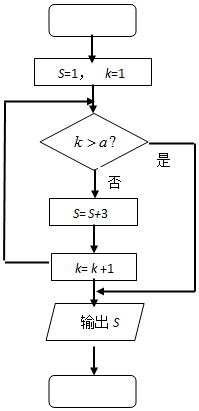

| A. | 2 | B. | 3 | C. | 4 | D. | 5 |