题目内容
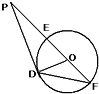如图，已知P是⊙O外一点，PD为⊙O的切线，D为切点，割线PEF经过圆心O．若PF=16，PD=4| 3 |
| A、13 | B、6.5 | C、7 | D、8 |
考点：与圆有关的比例线段
专题：立体几何
分析：由切割线定理得PD2=PE•PF，由此能求出圆的半径．
解答：
解：设⊙O的半径长为r，
∵P是⊙O外一点，PD为⊙O的切线，D为切点，
割线PEF经过圆心O．PF=16，PD=4
，
∴PD2=PE•PF，
∴（4
）2=（16-2r）×16，
解得r=6.5．
故选：B．
∵P是⊙O外一点，PD为⊙O的切线，D为切点，
割线PEF经过圆心O．PF=16，PD=4
| 3 |
∴PD2=PE•PF，
∴（4
| 3 |
解得r=6.5．
故选：B．
点评：本题考查圆的半径长的求法，解题时要认真审题，注意割线定理的合理运用．
练习册系列答案
文敬图书课时先锋系列答案
相关题目
f（x）=x-1，则f′（1）=（ ）
| A、1 | ||
B、
| ||
| C、-1 | ||
| D、0 |
在长为12的线段AB上任取一点M，并以线段AM为边作正三角形．此正三角形的面积介于9
与16
之间的概率（ ）
| 3 |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
将函数y=sin2x的图象向上平移1个单位长度，再向右平移1个单位长度，所得图象对应的函数解析式是（ ）
| A、y=2cos2x |
| B、y=2sin2x |
| C、y=1+sin2（x-1） |
| D、y=1+sin2（x+1） |
某人要制作一个三角形，要求它的三条高的长度分别为
，
，
，则此人能（ ）
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 7 |
| A、不能作出这样的三角形 |
| B、作出一个锐角三角形 |
| C、作出一个直角三角形 |
| D、作出一个钝角三角形 |
如图所示，直角三角形ABC中，∠ACB=90°，AC=2，BC=2| 2 |
| A、90° | B、45° |
| C、60° | D、30° |
已知△ABC三个内角A，B，C成等差数列，且AB=1，BC=4，则边AC上的高h=（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
抛物线y2=
x的焦点坐标是（ ）
| 1 |
| 4 |
| A、（1，0） | ||
B、（
| ||
| C、（0，1） | ||
D、（0，
|