题目内容
设数列{an}为等差数列,前n项和为Sn,已知a2=2,S5=15.
(Ⅰ)求{an}的通项公式;
(Ⅱ)若bn=an•2n,求数列{bn}的前n项和Tn.
(Ⅰ)求{an}的通项公式;
(Ⅱ)若bn=an•2n,求数列{bn}的前n项和Tn.
考点:数列的求和
专题:等差数列与等比数列
分析:(1)根据a2=2,S5=15,列出方程,求出等差数列{an}的首项和公差,然后求出an即可;
(2)根据题意,首先求出数列{bn}的通项bn,然后根据等比数列的求和公式,求出此数列的前n项和Gn即可.
(2)根据题意,首先求出数列{bn}的通项bn,然后根据等比数列的求和公式,求出此数列的前n项和Gn即可.
解答:
解:(1)∵
∴
∴
∴an=1+(n-1)=n,
即an=n.
(2)∵bn=an•2n,an=n
∴bn=n•2n,
数列{bn}的前n项和Tn=1•21+2•22+3•23+…+n•2n,
∴2Tn=1•22+2•23+3•24+…+(n-1)•2n+n•2n+1,
Tn-2Tn=21+22+23+…+2n-n2n+1=2n+1-2-n2n+1,
∴Tn=(n-1)2n+1+2.
|
∴
|
∴
|
∴an=1+(n-1)=n,
即an=n.
(2)∵bn=an•2n,an=n
∴bn=n•2n,
数列{bn}的前n项和Tn=1•21+2•22+3•23+…+n•2n,
∴2Tn=1•22+2•23+3•24+…+(n-1)•2n+n•2n+1,
Tn-2Tn=21+22+23+…+2n-n2n+1=2n+1-2-n2n+1,
∴Tn=(n-1)2n+1+2.
点评:本题主要考查了等差数列的通项公式,错位相减法求数列的和的运用,属于中档题.

练习册系列答案
相关题目
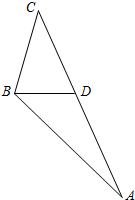 近日我渔船编队在钓鱼岛附近点A周围海域作业,在B处的海监15船测得A在其南偏东45°方向上,测得渔政船310在其北偏东15°方向上,且与B的距离为4
近日我渔船编队在钓鱼岛附近点A周围海域作业,在B处的海监15船测得A在其南偏东45°方向上,测得渔政船310在其北偏东15°方向上,且与B的距离为4