题目内容
函数f(x)=
的值域为 .
| |x|-1 |
| 2|x|+1 |
考点:函数的值域
专题:函数的性质及应用
分析:根据函数式子得出根据函数式子可判断在[0,+∞)单调递增,(-∞,0)单调递减,f(0)=-
,x→+∞,f(x)→
,求解即可.
| 5 |
| 2 |
| 1 |
| 2 |
解答:
解:∵函数f(x)=
∴f(x)=
-
,
∵f(-x)=f(x)
∴f(x)偶函数,
根据函数式子可判断在[0,+∞)单调递增,(-∞,0)单调递减,
f(0)=-
,
x→+∞,f(x)→
,
∴函数f(x)=
的值域为:[-
,
)
故答案为:[-
,
)
| |x|-1 |
| 2|x|+1 |
∴f(x)=
| 1 |
| 2 |
| 3 |
| 2|x|+1 |
∵f(-x)=f(x)
∴f(x)偶函数,
根据函数式子可判断在[0,+∞)单调递增,(-∞,0)单调递减,
f(0)=-
| 5 |
| 2 |
x→+∞,f(x)→
| 1 |
| 2 |
∴函数f(x)=
| |x|-1 |
| 2|x|+1 |
| 5 |
| 2 |
| 1 |
| 2 |
故答案为:[-
| 5 |
| 2 |
| 1 |
| 2 |
点评:本题考查了函数的性质,利用单调性,奇偶性求解函数值域,难度不大,属于容易题.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
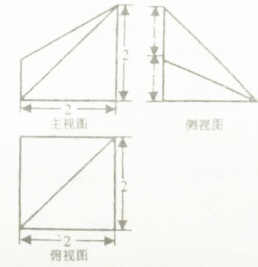
已知某几何体的三视图如图所示,则该几何体的体积为( )

A、
| ||||
| B、8 | ||||
C、
| ||||
D、
|
若函数f(x)=
+
,其中x∈[-
,a],若f(x)的值域是[-
,1],则a的取值范围是( )
| ||
| 2 |
| cos2x |
| 2 |
| π |
| 6 |
| 1 |
| 2 |
A、[-
| ||||
B、[-
| ||||
C、[
| ||||
D、[
|
设x∈(1,+∞),在函数f(x)=
的图象上,过点P(x,f(x))的切线在y轴上的截距为b,则b的最小值为( )
| x |
| lnx |
| A、e | ||
B、
| ||
C、
| ||
D、
|
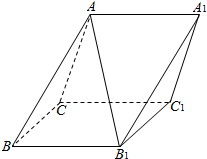 如图,在斜三棱柱ABC-A1B1C1中,侧面ACC1A1与侧面CBB1C1都是菱形,∠ACC1=∠CC1B1=60°,AC=2.
如图,在斜三棱柱ABC-A1B1C1中,侧面ACC1A1与侧面CBB1C1都是菱形,∠ACC1=∠CC1B1=60°,AC=2. 如图,在四棱锥ABCD-A1B1C1D1中,底面ABCD是等腰梯形,AB∥CD,AB=2,BC=CD=1,顶角D1在底面ABCD内的射影恰好为点C.
如图,在四棱锥ABCD-A1B1C1D1中,底面ABCD是等腰梯形,AB∥CD,AB=2,BC=CD=1,顶角D1在底面ABCD内的射影恰好为点C.