题目内容
1.已知x>0,当x+$\frac{4}{x}$取最小值时x的值为2.分析 由题意和基本不等式可得x+$\frac{4}{x}$≥2$\sqrt{x•\frac{4}{x}}$=4,由等号成立的条件可得x值.
解答 解:∵x>0,∴x+$\frac{4}{x}$≥2$\sqrt{x•\frac{4}{x}}$=4,
当且仅当x=$\frac{4}{x}$即x=2时上式取最小值4,
故答案为:2.
点评 本题考查基本不等式,属基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
16.已知x0是函数f(x)=2x-log0.5x的零点.则( )
| A. | 2x0<1<x0 | B. | x0<2x0<1 | C. | 1<x0<2x0 | D. | x0<1<2x0 |
6.若$\frac{5π}{2}$<α<3π,则$\sqrt{\frac{1}{2}+\frac{1}{2}\sqrt{\frac{1}{2}+\frac{1}{2}cosα}}$等于( )
| A. | cos$\frac{α}{4}$ | B. | -cos$\frac{α}{4}$ | C. | sin$\frac{α}{4}$ | D. | -sin$\frac{α}{4}$ |
10.在Rt△ABC中,∠A为直角,且AB=3,BC=5,若在三角形ABC内任取一点,则该点到三个定点A,B,C的距离不小于1的概率是( )
| A. | $\frac{π}{6}$ | B. | 1-$\frac{π}{6}$ | C. | $\frac{π}{12}$ | D. | 1-$\frac{π}{12}$ |
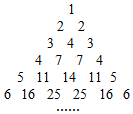 如图三角形数阵满足:
如图三角形数阵满足: