题目内容
2.写出函数$y=\sqrt{3}{sin^2}x+2sinxcosx-\sqrt{3}{cos^2}x$的值域、单调递增区间、对称轴方程、对称中心坐标(只需写出答案即可),并用五点法作出该函数在一个周期内的图象.分析 先化简f(x)的解析式,根据正弦函数的图象与性质列出不等式或等式得出各结论.
解答 解:y=-$\sqrt{3}$(cos2x-sin2x)+2sinxcosx=-$\sqrt{3}$cos2x+sin2x=2sin(2x-$\frac{π}{3}$),
∴函数的值域:[-2,2];
令-$\frac{π}{2}$+2kπ≤2x-$\frac{π}{3}$≤$\frac{π}{2}$+2kπ,解得-$\frac{π}{12}$+kπ≤x≤$\frac{5π}{12}$+kπ,
∴函数的递增区间:$[kπ-\frac{π}{12},kπ+\frac{5π}{12}]$,k∈Z;
令2x-$\frac{π}{3}$=$\frac{π}{2}+kπ$,解得x=$\frac{5π}{12}$+$\frac{kπ}{2}$,
∴函数的对称轴:x=$\frac{5π}{12}$+$\frac{kπ}{2}$,k∈Z;
令2x-$\frac{π}{3}$=kπ得x=$\frac{π}{6}$+$\frac{kπ}{2}$,
∴函数的对称中心:($\frac{π}{6}$+$\frac{kπ}{2}$,0),k∈Z;
作图如下:
(1)列表:
| 2x-$\frac{π}{3}$ | 0 | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | 2π |
| x | $\frac{π}{6}$ | $\frac{5π}{12}$ | $\frac{2π}{3}$ | $\frac{11π}{12}$ | $\frac{7π}{6}$ |
| y | 0 | 2 | 0 | -2 | 0 |

点评 本题考查了三角恒等变换,正弦函数的图象与性质,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.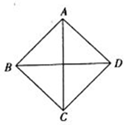 已知某几何体是由两个四棱锥组合而成,若该几何体的正视图、俯视图和侧视图均为如图所示的图形,其中四边形是边长为$\sqrt{2}$的正方形,则该几何体的表面积是( )
已知某几何体是由两个四棱锥组合而成,若该几何体的正视图、俯视图和侧视图均为如图所示的图形,其中四边形是边长为$\sqrt{2}$的正方形,则该几何体的表面积是( )
 已知某几何体是由两个四棱锥组合而成,若该几何体的正视图、俯视图和侧视图均为如图所示的图形,其中四边形是边长为$\sqrt{2}$的正方形,则该几何体的表面积是( )
已知某几何体是由两个四棱锥组合而成,若该几何体的正视图、俯视图和侧视图均为如图所示的图形,其中四边形是边长为$\sqrt{2}$的正方形,则该几何体的表面积是( )| A. | 8$\sqrt{3}$ | B. | 4$\sqrt{3}$ | C. | 8$\sqrt{3}$+2 | D. | 4$\sqrt{3}$+2 |
12.某产品的广告费用x(百万元)与销售额y(百万元)的统计数据如表:
根据表中数据,用最小二乘法得出y与x的线性回归方程为$\stackrel{∧}{y}$=8.6x+5,则表中的m的值为( )
| x | 2 | 3 | 4 | 7 | 9 |
| y | 26 | 33 | m | 54 | 75 |
| A. | 46 | B. | 48 | C. | 50 | D. | 52 |