题目内容
11.在△ABC中,a,b,c分别为三个内角A,B,C的对边,若$cosBcosC-sinBsinC=\frac{1}{2}$,$a=2\sqrt{3}$(1)求A;
(2)若b=2,求c边长;
(3)若b+c=4,求△ABC的面积.
分析 (1)利用和差公式、三角函数的单调性即可得出.
(2)利用余弦定理即可得出.
(3)根据余弦定理,得(2$\sqrt{3}$)2=b2+c2-2bccos $\frac{2π}{3}$,化为12=b2+c2+bc,又b+c=4,解得bc,再利用三角形面积计算公式即可得出.
解答 解:(1)因为cos Bcos C-sin Bsin C=$\frac{1}{2}$,
所以cos(B+C)=$\frac{1}{2}$,
又因为0<B+C<π,所以B+C=$\frac{π}{3}$,即A=π-(B+C)=$\frac{2π}{3}$.
(2)由余弦定理可得:(2$\sqrt{3}$)2=b2+c2-2bccos $\frac{2π}{3}$,所以12=4+c2+2c,
化为:c2+2c-8=0,c>0,解得c=2.
(3)根据余弦定理,
得(2$\sqrt{3}$)2=b2+c2-2bccos $\frac{2π}{3}$,所以12=b2+c2+bc,
即12=(b+c)2-bc.
又b+c=4,
所以12=42-bc⇒bc=4.
所以S△ABC=$\frac{1}{2}$bcsin A=$\frac{1}{2}$×4×$\frac{\sqrt{3}}{2}$=$\sqrt{3}$.
点评 本题考查了和差公式、三角函数的单调性、余弦定理、三角形面积计算公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
6.若数列{an}满足$\frac{1}{{{a_{n+1}}}}-\frac{1}{a_n}=d$(n∈N*,d为常数),则称{an}为“调和数列”,已知正项数列$\left\{{\frac{1}{x_n}}\right\}$为“调和数列”,且x1+x2+…+x20=200,则$\frac{1}{x_3}+\frac{1}{{{x_{18}}}}$的最小值为( )
| A. | $\frac{1}{10}$ | B. | 10 | C. | $\frac{1}{5}$ | D. | 5 |
20.已知函数f(x)=ax2-c满足:-4≤f(1)≤-1,-1≤f(2)≤5,则f(3)应满足( )
| A. | -7≤f(3)≤26 | B. | -4≤f(3)≤15 | C. | -1≤f(3)≤20 | D. | $-\frac{28}{3}≤f(3)≤\frac{35}{3}$ |
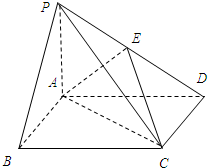 如图,四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AB=1,BC=2,E为PD的中点.
如图,四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AB=1,BC=2,E为PD的中点.