题目内容
7.已知函数f(x)=log2(x-2)+$\sqrt{x-1}$.(1)求函数f(x)的定义域;
(2)求f(3),f(10)的值.
分析 (1)由对数式的真数部分大于零点,被开方数不小于0,构造不等式组,解得函数的定义域;
(2)根据已知中函数的解析式,将x=3和x=10代入计算可得对应的函数值.
解答 解:(1)由$\left\{\begin{array}{l}x-2>0\\ x-1≥0\end{array}\right.$得x∈(2,+∞),
∴函数f(x)=log2(x-2)+$\sqrt{x-1}$的定义域为(2,+∞)…(4分)
(2)f(3)=log2(3-2)+$\sqrt{3-1}$=$\sqrt{2}$ …(7分)
f(10)=log2(10-2)+$\sqrt{10-1}$=6…(10分)
点评 本题考查的知识点是对数函数的图象和性质,熟练掌握对数函数的图象和性质是解答的关键.

练习册系列答案
相关题目
2.若函数f(x)=x2+ax+blnx+c有三个不同的零点x1,x2,x3且x1<x2<x3的若x=m是f(x)的极大值点,且f(m)=x3,则关于x的方程f[f(x)]=0的不同零点的个数是( )
| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
13.函数$y={log_{\frac{1}{2}}}$(ax+2)在[-1,3]上递增,则a的取值范围是( )
| A. | (-∞,0) | B. | $(-\frac{2}{3},0)$ | C. | (-1,0) | D. | (-3,-1) |
14.在等比数列,${S_n}={3^n}-1$,则a1等于( )
| A. | 2 | B. | 3 | C. | 6 | D. | 8 |
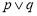 为真”是“
为真”是“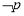 为假”的( )条件
为假”的( )条件 ,若存在实数
,若存在实数 满足
满足 其中
其中 ,则
,则 的取值范围是( )
的取值范围是( ) B.
B.
 D.
D.
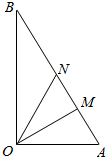 如图所示,某镇有一块空地△OAB,其中$OA=3km,OB=3\sqrt{3}km$,∠AOB=90°.当地镇政府规划将这块空地改造成一个旅游景点,拟在中间挖一个人工湖△OMN,其中M,N都在边A,B上,且∠MON=30°,挖出的泥土堆放在△OAM地带上形成假山,剩下的△OBN地带开设儿童游乐场.为了安全起见,需在△OAN的一周安装防护网.
如图所示,某镇有一块空地△OAB,其中$OA=3km,OB=3\sqrt{3}km$,∠AOB=90°.当地镇政府规划将这块空地改造成一个旅游景点,拟在中间挖一个人工湖△OMN,其中M,N都在边A,B上,且∠MON=30°,挖出的泥土堆放在△OAM地带上形成假山,剩下的△OBN地带开设儿童游乐场.为了安全起见,需在△OAN的一周安装防护网.