题目内容
17.(理科)极坐标系中两点$A(3,\frac{π}{6})$,$B(1,\frac{π}{2})$,则线段AB的长等于$\sqrt{7}$.分析 根据极坐标系中两点间的距离公式,求出线段AB的长即可.
解答 解:极坐标系中$A(3,\frac{π}{6})$,$B(1,\frac{π}{2})$,
∴线段AB的长为
|AB|=$\sqrt{{3}^{2}{+1}^{2}-2×3×1×cos(\frac{π}{2}-\frac{π}{6})}$=$\sqrt{7}$.
故答案为:$\sqrt{7}$.
点评 本题考查了极坐标系中两点间的距离公式的应用问题,是基础题目.

练习册系列答案
相关题目
5.已知函数f(x)=2loga(x-1)(a>0且a≠1)恒过点(m,n),则在直角坐标系中,函数$g(x)={(\frac{1}{m+n})^{|{x+1}|}}$的大致图象为( )
| A. | 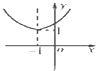 | B. | 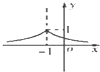 | C. | 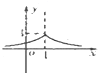 | D. | 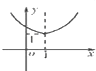 |
6.已知向量$\overrightarrow{a}$=(1,2),$\overrightarrow{b}$=(x,-2),且$\overrightarrow{a}$∥$\overrightarrow{b}$,则向量$\overrightarrow{a}$-$\overrightarrow{b}$的模为( )
| A. | 5 | B. | $2\sqrt{5}$ | C. | $2\sqrt{2}$ | D. | $\sqrt{2}$ |
 为偶函数,当
为偶函数,当 时,
时, ,则曲线
,则曲线 在
在 处的切线方程式为______________.
处的切线方程式为______________. )的图象可看成是把函数y=sin2x的图象作以下平移得到 ( )
)的图象可看成是把函数y=sin2x的图象作以下平移得到 ( )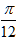 D.向左平移
D.向左平移