题目内容
函数y=f(x)的最小正周期为2,且f(-x)=f(x).当x∈[0,1]时f(x)=-x+1,那么在区间[-3,4]上,函数G(x)=f(x)-(
)|x|的零点个数有 个.
| 1 |
| 2 |
考点:函数零点的判定定理
专题:函数的性质及应用
分析:函数G(x)=f(x)-(
)|x|的零点个数即为y=f(x)与y=(
)|x|的图象的交点个数,只要由函数的性质,在同一个坐标系中作出两个函数的图象,即可的答案.
| 1 |
| 2 |
| 1 |
| 2 |
解答:
解:由题意可知,函数G(x)=f(x)-(
)|x|的零点个数即为y=f(x)与y=(
)|x|的图象的交点个数,
函数y=f(x)周期为2,且为偶函数,函数y=(
)|x|为偶函数,
在同一个坐标系中作出它们的图象,

可得交点个数为6,
故答案为:6.
| 1 |
| 2 |
| 1 |
| 2 |
函数y=f(x)周期为2,且为偶函数,函数y=(
| 1 |
| 2 |
在同一个坐标系中作出它们的图象,

可得交点个数为6,
故答案为:6.
点评:本题考查由函数的性质作函数的图象,以及函数的零点问题转化成两函数图象的交点问题,同时考查了作图的能力,属中档题.

练习册系列答案
相关题目
曲线y=xex+2x+1在点(0,1)处的切线方程为( )
| A、x+3y-3=0 |
| B、3x-y+1=0 |
| C、3x+y-1=0 |
| D、x-3y+3=0 |
 如图,正方体ABCD-A1B1C1D1中,E、F分别为棱AB、CC1的中点,画出平面D1EF与平面ADD1A1的交线.
如图,正方体ABCD-A1B1C1D1中,E、F分别为棱AB、CC1的中点,画出平面D1EF与平面ADD1A1的交线.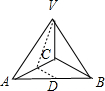 在三棱锥V-ABC中,D、E分别为AB,AC的中点,平面VCB⊥平面ABC,AC⊥BC.
在三棱锥V-ABC中,D、E分别为AB,AC的中点,平面VCB⊥平面ABC,AC⊥BC. 已知函数f(x)=Asin(ωx+φ),(A>0,ω>0,0<φ<π)的图象如图
已知函数f(x)=Asin(ωx+φ),(A>0,ω>0,0<φ<π)的图象如图