题目内容
已知数列{an}的前n项和为Sn,满足Sn=2an-1(n∈N*).
(1)求数列{an}的通项公式;
(2)证明:
<
+
+…+
<1(n∈N*).
(1)求数列{an}的通项公式;
(2)证明:
| 1 |
| 2 |
| 1 |
| a2 |
| 1 |
| a3 |
| 1 |
| an+1 |
考点:数列的求和,数列递推式
专题:等差数列与等比数列
分析:(1)利用递推式与等比数列的通项公式即可得出;
(2)利用等比数列的前n项和公式及其数列的单调性即可得出.
(2)利用等比数列的前n项和公式及其数列的单调性即可得出.
解答:
(1)解:∵Sn=2an-1(n∈N*),
∴当n=1时,a1=2a1-1,解得a1=1.
当n≥2时,an=Sn-Sn-1=2an-1-(2an-1-1)=2an-2an-1,
∴an=2an-1,
∴数列{an}是等比数列,首项为1,公比为2.
∴an=2n-1.
(2)证明:∵an=2n-1,
∴
=
.
∴
+
+…+
=
+
+…+
=
=1-
.
∵数列{1-
}单调递增,
∴
≤1-
<1.
∴
<
+
+…+
<1(n∈N*).
∴当n=1时,a1=2a1-1,解得a1=1.
当n≥2时,an=Sn-Sn-1=2an-1-(2an-1-1)=2an-2an-1,
∴an=2an-1,
∴数列{an}是等比数列,首项为1,公比为2.
∴an=2n-1.
(2)证明:∵an=2n-1,
∴
| 1 |
| an |
| 1 |
| 2n-1 |
∴
| 1 |
| a2 |
| 1 |
| a3 |
| 1 |
| an+1 |
=
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 2n |
=
| ||||
1-
|
=1-
| 1 |
| 2n |
∵数列{1-
| 1 |
| 2n |
∴
| 3 |
| 4 |
| 1 |
| 22 |
∴
| 1 |
| 2 |
| 1 |
| a2 |
| 1 |
| a3 |
| 1 |
| an+1 |
点评:本题考查了递推式、等比数列的通项公式及其前n项和公式、数列的单调性,考查了推理能力与几十年令,属于中档题.

练习册系列答案
相关题目
等差数列{an}的公差d≠0,a1=20,且a3,a7,a9成等比数列.Sn为{an}的前n项和,则S10的值为( )
| A、-110 | B、-90 |
| C、90 | D、110 |
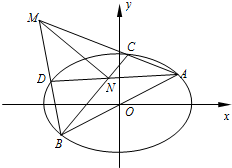 如图,在平面直角坐标系xoy中,椭圆E:
如图,在平面直角坐标系xoy中,椭圆E: 如图,四棱锥P-ABCD的底面是直角梯形,∠ABC=∠BCD=90°,BC=PB=PC,PO⊥AD,O为BC的中点.
如图,四棱锥P-ABCD的底面是直角梯形,∠ABC=∠BCD=90°,BC=PB=PC,PO⊥AD,O为BC的中点.