题目内容
有标号为1、2、3、4、5、的五个红球和标号为1、2的两个白球,将这七个球排出一排,使两端都是红球.
(1)如果每个白球的两边都是红球,有多少种排法?
(2)如果1号红球和1号白球相邻排在一起,有多少种排法?
(3)同时满足上述两个条件的排法是多少种?
(1)如果每个白球的两边都是红球,有多少种排法?
(2)如果1号红球和1号白球相邻排在一起,有多少种排法?
(3)同时满足上述两个条件的排法是多少种?
考点:排列、组合及简单计数问题
专题:排列组合
分析:(1)利用抽空法,按照先特殊再一般的原则进行排列即可.
(2)采用捆绑法把1号红球和1号白球当作一个元素要注意它本身的顺序.
(3)结合(1)(2)的做法进行排列即可.
(2)采用捆绑法把1号红球和1号白球当作一个元素要注意它本身的顺序.
(3)结合(1)(2)的做法进行排列即可.
解答:
解:(1)利用抽空法,先排5个红球,再将2个白球插入到所形成的4个间隔(不包含两端)中,故有
•
=1440种;
(2)把1号红球和1号白球捆绑在一起,第一类,先排2个红球在两端,剩下2个红球和2号白球以及复合元素(1号红球和1号白球),进行全排列,故有
•
•
=576种,
第二类,1号红球排在两端,先排列剩下4个红球,再插入2号白球,故有
•
•
=192种,
根据分类计数原理,故有576+192=768种;
(3)把1号红球和1号白球捆绑在一起,看作一个复合元素,
第一类,当1号红球排在两端,先排列剩下4个红球,再插入2号白球,且满足每个白球的两边都是红球,故有
•
•
=144种,
第二类,当1号红球排在不在两端时,且不与2号白球相邻,先排列剩下4个红球,再插入复合元素和2号白球,故有
•
•
=288种,
第三类,当1号红球排在不在两端时,且与2号白球相邻,先把两个白球捆绑在1号红球两边看一个复合元素,插入到剩下4个红球排列形成的三个间隔中,故有
•
=144种,
根据分类计数原理,故有144+288+144=576种.
| A | 5 5 |
| A | 2 4 |
(2)把1号红球和1号白球捆绑在一起,第一类,先排2个红球在两端,剩下2个红球和2号白球以及复合元素(1号红球和1号白球),进行全排列,故有
| A | 2 2 |
| A | 2 4 |
| A | 4 4 |
第二类,1号红球排在两端,先排列剩下4个红球,再插入2号白球,故有
| A | 1 2 |
| A | 4 4 |
| A | 1 4 |
根据分类计数原理,故有576+192=768种;
(3)把1号红球和1号白球捆绑在一起,看作一个复合元素,
第一类,当1号红球排在两端,先排列剩下4个红球,再插入2号白球,且满足每个白球的两边都是红球,故有
| A | 1 2 |
| A | 4 4 |
| A | 1 3 |
第二类,当1号红球排在不在两端时,且不与2号白球相邻,先排列剩下4个红球,再插入复合元素和2号白球,故有
| A | 4 4 |
| A | 1 2 |
| A | 2 3 |
第三类,当1号红球排在不在两端时,且与2号白球相邻,先把两个白球捆绑在1号红球两边看一个复合元素,插入到剩下4个红球排列形成的三个间隔中,故有
| A | 2 2 |
| •A | 4 4 |
| A | 1 3 |
根据分类计数原理,故有144+288+144=576种.
点评:本题考查了分类计数原理以及相邻问题用捆绑,不相邻问题用插空,关键是如何分类,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
某几何体的三视图如图,则该几何体的表面积为( )


| A、24 | B、36 | C、48 | D、60 |
若平面向量
,
满足|
+
|=1,且
=2
,则|
|=( )
| a |
| b |
| a |
| b |
| a |
| b |
| b |
A、
| ||
B、
| ||
| C、1 | ||
D、
|
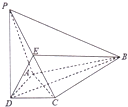 如图,在四棱锥P-ABCD中,PD⊥平面ABCD,AD⊥DC,DB平分∠ADC,E为PC的中点,AD=CD=1,DB=2
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,AD⊥DC,DB平分∠ADC,E为PC的中点,AD=CD=1,DB=2