题目内容
已知f(x)=x+log2
,则f(1)+f(2)+f(3)+…+f(8)的值为 .
| x |
| 9-x |
考点:函数的值
专题:函数的性质及应用
分析:根据函数的性质找出规律f(x)+f(9-x)=9,由此能求出f(1)+f(2)+f(3)+…+f(8)的值.
解答:
解:由于f(x)=x+log2
,
所以f(9-x)=9-x+log2
=9-x-log2
,
于是有f(x)+f(9-x)=9,
从而f(1)+f(8)=f(2)+f(7)=f(3)+f(6)=f(4)+f(5)=9,
故原式的值为4×9=36.
| x |
| 9-x |
所以f(9-x)=9-x+log2
| 9-x |
| x |
| x |
| 9-x |
于是有f(x)+f(9-x)=9,
从而f(1)+f(8)=f(2)+f(7)=f(3)+f(6)=f(4)+f(5)=9,
故原式的值为4×9=36.
点评:本题考查函数值的求法,是基础题,解题时要认真审题,解题的关键是推导出f(x)+f(9-x)=9.

练习册系列答案
相关题目
函数f(x)=[x]的函数值表示不超过x的最大整数,例如,[-3.5]=-4,[2.1]=2.当x∈(-2.5,3]时,函数f(x)的值域为( )
| A、{-2,-1,0,1,2} |
| B、{-3,-2,-1,0,1,2} |
| C、{-2,-1,0,1,2,3} |
| D、{-3,-2,-1,0,1,2,3} |
已知集合A={z||z|≤2,z∈C},集合B={z|z=1+ai,a∈R},其中C为复数集,i为虚数单位,若A∩B≠∅,则实数a的取值范围是( )
A、(-∞,-
| ||||
B、(-
| ||||
C、(-∞,-
| ||||
D、[-
|
程序框图如图所示,该程序运行后输出的S的值是( )


A、
| ||
| B、-3 | ||
C、-
| ||
| D、2 |
设全集为实数集R,M={x|x2>4},N={x|1<x≤3},则图中阴影部分表示的集合是( ) 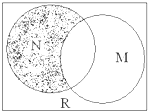

| A、{x|1-2≤x<1} |
| B、{x|-2≤x≤2} |
| C、{x|1<x≤2} |
| D、{x|x<2} |
集合A={x|y=ln(-x2+2x+3)},B={y|y=ex},则A∩B=( )
| A、{x|-1<x<0} |
| B、{x|0<x<3} |
| C、{x|x>-1} |
| D、{x|x<3} |