题目内容
8.(1)已知$f(x)=\left\{\begin{array}{l}{2^x}+3,({x≤0})\\{({x-2})^2},({x>0})\end{array}\right.$在区间(m2-4m,2m-2)上能取得最大值,求实数m的取值范围;(2)设函数f(x)=ax-(k-1)a-x(a>0且a≠1)是定义域为R的奇函数,若$f(1)=\frac{3}{2}$,且g(x)=a2x+a-2x-2m•f(x)在[1,+∞)上的最小值为-2,求m的值.
分析 (1)作函数$f(x)=\left\{\begin{array}{l}{2^x}+3,x≤0\\{({x-2})^2},x>0\end{array}\right.$的图象,在区间(m2-4m,2m-2)上能取得最大值,可得,$\left\{\begin{array}{l}{m^2}-4m<0\\ 0<2m-2≤4\end{array}\right.$,即可求实数m的取值范围;
(2)求出f(x)=2x-2-x,g(x)=22x+2-2x-2m(2x-2-x),再根据g(x)=a2x+a-2x-2m•f(x)在[1,+∞)上的最小值为-2,即可求m的值.
解答 解:(1)作函数$f(x)=\left\{\begin{array}{l}{2^x}+3,x≤0\\{({x-2})^2},x>0\end{array}\right.$的图象如下,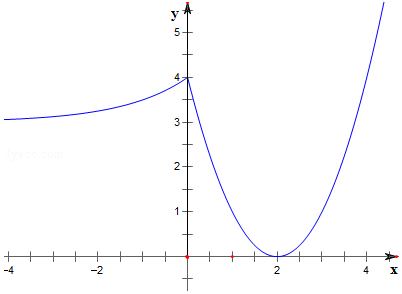
结合图象可知,$\left\{\begin{array}{l}{m^2}-4m<0\\ 0<2m-2≤4\end{array}\right.$;解得1<m≤3;
故实数m的取值范围为(1,3];
(2)由题意,对任意x∈R,f(-x)=-f(x)
即a-x-(k-1)ax=-ax+(k-1)a-x,
即(k-1)(ax+a-x)-(ax+a-x)=0,(k-2)(ax+a-x)=0,
因为x为任意实数,所以k=2.
∵f(x)=ax-a-x,∴$f(1)=\frac{3}{2}$,∴$a-\frac{1}{a}=\frac{3}{2}$,解得a=2.
故f(x)=2x-2-x,g(x)=22x+2-2x-2m(2x-2-x),
令t=2x-2-x,易得t为增函数,由x∈[1,+∞),得$t∈[{\frac{3}{2},+∞})$,
则22x+2-2x=t2+2,∴$g(x)=h(t)={t^2}-2mt+2={({t-m})^2}+2-{m^2},t∈[{\frac{3}{2},+∞})$.
当$m<\frac{3}{2}$时,h(t)在$[{\frac{3}{2},+∞})$上是增函数,则$h({\frac{3}{2}})=-2,\frac{9}{4}-3m+2=-2$,
解得$m=\frac{25}{12}$(舍去).当$m≥\frac{3}{2}$时,h(m)2-m2=-2,解得m=2,或m=-2(舍去).
综上,m的值是2.
点评 本题考查函数的最值,考查函数的单调性,考查数形结合的数学思想,属于中档题.

| A. | mx+m2y-1=0 | B. | x+y+3=0 | C. | x-y-3=0 | D. | x+y-3=0 |
| A. | ($\frac{1}{e}$,2)∪(2,e) | B. | ($\frac{1}{e}$+1,e) | C. | (e-1,e) | D. | ($\frac{1}{e}$,e) |
| A. | 可以小于0 | B. | 只能大于0 | C. | 可以为0 | D. | 只能小于0 |
| A. | sinα-cosα>1 | B. | sinα-cosα=1 | C. | sinα-cosα<1 | D. | 不能确定 |