题目内容
20.已知有线性相关关系的两个变量建立的回归直线方程为$\stackrel{∧}{y}$=$\stackrel{∧}{a}$+$\stackrel{∧}{b}$x,方程中的回归系数$\stackrel{∧}{b}$( )| A. | 可以小于0 | B. | 只能大于0 | C. | 可以为0 | D. | 只能小于0 |
分析 根据相关系数知$\stackrel{∧}{b}$=0时,r=0,当r的绝对值接近于零时,表示两个变量之间几乎不存在线性相关关系,$\stackrel{∧}{b}$不能等于零,$\stackrel{∧}{b}$能大于0也能小于0.选出正确结果.
解答 解:$\stackrel{∧}{b}$=0时,r=0,当r的绝对值接近于零时,表示两个变量之间几乎不存在线性相关关系,
∴$\stackrel{∧}{b}$不能等于零,$\stackrel{∧}{b}$能大于0也能小于0.
故选A.
点评 本题考查用相关系数来衡量两个变量之间相关关系的方法,当相关系数为正时,表示两个变量正相关,当相关系数大于0.75时,表示两个变量有很强的线性相关关系.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
11.设函数f(x)在R上存在导数f′(x),?x∈R,有f(-x)+f(x)=x2,在(0,+∞)上f′(x)<x,若f(2-m)+f(-m)-m2+2m-2≥0,则实数m的取值范围为( )
| A. | [-1,1] | B. | [1,+∞) | C. | [2,+∞) | D. | (-∞,-2]∪[2,+∞) |
12.已知复数z=1-i(i为虚数单位),则$\frac{2}{z}-{z^2}$的共轭复数是( )
| A. | 1-3i | B. | 1+3i | C. | -1+3i | D. | -1-3i |
9.已知tanθ=-3,则$\frac{sinθ-2cosθ}{cosθ+sinθ}$的值为( )
| A. | $-\frac{2}{5}$ | B. | $\frac{2}{5}$ | C. | $-\frac{5}{2}$ | D. | $\frac{5}{2}$ |
5. 如图,在四面体P-ABC中,PA=PB=PC=4,点O是点P在平面ABC上的投影,且tan∠APO=$\frac{\sqrt{2}}{2}$,则四面体P-ABC的外接球的体积为( )
如图,在四面体P-ABC中,PA=PB=PC=4,点O是点P在平面ABC上的投影,且tan∠APO=$\frac{\sqrt{2}}{2}$,则四面体P-ABC的外接球的体积为( )
 如图,在四面体P-ABC中,PA=PB=PC=4,点O是点P在平面ABC上的投影,且tan∠APO=$\frac{\sqrt{2}}{2}$,则四面体P-ABC的外接球的体积为( )
如图,在四面体P-ABC中,PA=PB=PC=4,点O是点P在平面ABC上的投影,且tan∠APO=$\frac{\sqrt{2}}{2}$,则四面体P-ABC的外接球的体积为( )| A. | 8$\sqrt{6}$π | B. | 24π | C. | 32$\sqrt{3}$π | D. | 48π |
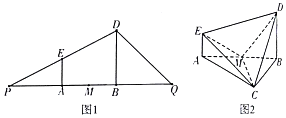 已知△PDQ中,A,B分别为边PQ上的两个三等分点,BD为底边PQ上的高,AE∥DB,如图1,将△PDQ分别沿AE,DB折起,使得P,Q重合于点C.AB中点为M,如图2.
已知△PDQ中,A,B分别为边PQ上的两个三等分点,BD为底边PQ上的高,AE∥DB,如图1,将△PDQ分别沿AE,DB折起,使得P,Q重合于点C.AB中点为M,如图2.