题目内容
3.已知函数f(x)=ln(2ax+1)+$\frac{x^3}{3}-{x^2}-2ax({a∈R})$.(1)若y=f(x)在[3,+∞)上为增函数,求实数a的取值范围;
(2)当a=-$\frac{1}{2}$时,函数y=f(1-x)-$\frac{{{{({1-x})}^3}}}{3}-\frac{b}{x}$有零点,求实数b的最大值.
分析 (1)利用函数f(x)在区间[3,+∞)上为增函数,导函数的符号,通过①当a=0时,②当a≠0时,说明只能a>0,利用函数的单调性以及最值求解a的取值范围.
(2)当$a=-\frac{1}{2}$时,函数$y=f({1-x})-\frac{{{{({1-x})}^3}}}{3}-\frac{b}{x}$有零点等价于方程:$f({1-x})=\frac{{{{({1-x})}^2}}}{3}+\frac{b}{x}$有实根,$f({1-x})=\frac{{{{({1-x})}^3}}}{3}+\frac{b}{x}$可化为:$lnx-{({1-x})^2}+({1-x})-\frac{b}{x}$=0.等价于b=xlnx+x2-x3在(0,+∞)上有解,
令函数h(x)=lnx+x-x2(x>0),求解$h'(x)=\frac{1}{x}+1-2x=\frac{{({2x+1})({1-x})}}{x}$,求出函数的最值,推出结果即可.
解答 解:(1)∵函数f(x)在区间[3,+∞)上为增函数,
∴$f'(x)=\frac{{x[{2a{x^2}+x-4ax-4{a^2}-2}]}}{2ax+1}≥0$在区间[3,+∞)上恒成立,
①当a=0时,f'(x)=x(x-2)≥0在[3,+∞)上恒成立,
∴f(x)在[3,+∞)上为增函数,故a=0符合题意.
②当a≠0时,由函数f(x)的定义域可知2ax+1>0对x≥3恒成立,
故只能a>0,∴2ax2+(1-4a)x-(4a2+2)≥0在[3,+∞)上恒成立,
令函数g(x)=2ax2+(1-4a)x-(4a2+2),其对称轴为$x=1-\frac{1}{4a}$,
∵a>0,∴$1-\frac{1}{4a}<1$,要使g(x)≥0在[3,+∞)上恒成立,只要g(3)≥0即可,
即g(3)=-4a2+6a+1≥0,∴$\frac{{3-\sqrt{13}}}{4}≤a≤\frac{{3+\sqrt{13}}}{4}$,
∵a>0,∴$0<a≤\frac{{3+\sqrt{13}}}{4}$,综上所述,a的取值范围为$0<a≤\frac{{3+\sqrt{13}}}{4}$.
(2)当$a=-\frac{1}{2}$时,函数$y=f({1-x})-\frac{{{{({1-x})}^3}}}{3}-\frac{b}{x}$有零点,
等价于方程:$f({1-x})=\frac{{{{({1-x})}^2}}}{3}+\frac{b}{x}$有实根,$f({1-x})=\frac{{{{({1-x})}^3}}}{3}+\frac{b}{x}$
可化为:$lnx-{({1-x})^2}+({1-x})-\frac{b}{x}$=0.
等价于b=xlnxx-x(1-x)2+x(1-x)=xlnx+x2-x3在(0,+∞)上有解,
即求函数g(x)=xlnx+x2-x3的值域,
∵函数g(x)=x(lnx+x-x2),
令函数h(x)=lnx+x-x2(x>0),则$h'(x)=\frac{1}{x}+1-2x=\frac{{({2x+1})({1-x})}}{x}$,
∴当0<x<1时,h'(x)>0,从而函数h(x)在(0,1)上为增函数,
当x>1时,h'(x)<0,从而函数h(x)在(1,+∞)上为减函数,
因此h(x)≤h(1)=0,而x>0,∴b=x•h(x)≤0,
故当x=1时,b取得最大值0.
点评 本题考查函数的导数的应用,函数的单调性以及函数的极值最值的求法,同时考查转化思想以及计算能力.

| A. | $\frac{1}{3}$ | B. | $\frac{5}{9}$ | C. | $\frac{2}{3}$ | D. | $\frac{7}{9}$ |
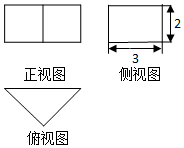
| A. | 18 | B. | $18\sqrt{3}$ | C. | $6\sqrt{3}$ | D. | $12\sqrt{3}$ |
| A. | [-1,1] | B. | [1,+∞) | C. | [2,+∞) | D. | (-∞,-2]∪[2,+∞) |
| A. | 1-3i | B. | 1+3i | C. | -1+3i | D. | -1-3i |
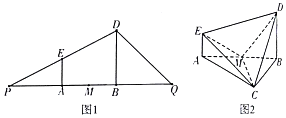 已知△PDQ中,A,B分别为边PQ上的两个三等分点,BD为底边PQ上的高,AE∥DB,如图1,将△PDQ分别沿AE,DB折起,使得P,Q重合于点C.AB中点为M,如图2.
已知△PDQ中,A,B分别为边PQ上的两个三等分点,BD为底边PQ上的高,AE∥DB,如图1,将△PDQ分别沿AE,DB折起,使得P,Q重合于点C.AB中点为M,如图2.