题目内容
9．若函数f（x）满足f（x）=x2lnx+3xf′（1）-1，则f′（1）等于（ ）| A． | -$\frac{1}{2}$ | B． | -$\frac{1}{3}$ | C． | -1 | D． | 1 |
分析 求函数的导数，令x=1即可得到结论．
解答 解：函数的导数f′（x）=2xlnx+x2$•\frac{1}{x}$+3f′（1）=2xlnx+x+3f′（1），
令x=1，则f′（1）=1+3f′（1），
即2f′（1）=-1，f′（1）=-$\frac{1}{2}$，
故选：A．
点评 本题主要考查函数的导数的计算，根据函数的导数公式建立方程关系是解决本题的关键．比较基础．
练习册系列答案
相关题目
19．某企业为了研究员工工作积极性和对待企业改革态度的关系，随机抽取了80名员工进行调查，所得的数据如表所示：
根据上述数据能得出的结论是（参考公式与数据：${Χ^2}=\frac{{n{{（ad-bc）}^2}}}{（a+b）（b+c）（a+c）（b+d）}$（其中n=a+b+c+d）；当Χ2＞3.841时，有95%的把握说事件A与B有关；当Χ2＞6.635时，有99%的把握说事件A与B有关； 当Χ2＜3.841时认为事件A与B无关．）（ ）
| 积极支持改革 | 不太支持改革 | 合 计 | |
| 工作积极 | 50 | 10 | 60 |
| 工作一般 | 10 | 10 | 20 |
| 合 计 | 60 | 20 | 80 |
| A． | 有99%的把握说事件A与B有关 | B． | 有95%的把握说事件A与B有关 | ||
| C． | 有90%的把握说事件A与B有关 | D． | 事件A与B无关 |
20．下列函数中，在区间（-1，$\frac{π}{2}$）上单调递减的函数为（ ）
| A． | y=x2 | B． | y=3x-1 | C． | y=log2（x+1） | D． | y=-sinx |
4．已知集合B={x|-3＜x＜2}，C={x|2x-1≥0}．
（1）求B∩C，B∪C；
（2）设函数f（x）=$\sqrt{lo{g}_{2}（2x+m）}$的定义域为A，且A⊆C，求实数m的最大值．
（1）求B∩C，B∪C；
（2）设函数f（x）=$\sqrt{lo{g}_{2}（2x+m）}$的定义域为A，且A⊆C，求实数m的最大值．
14．下列等式不正确的是（ ）
| A． | ${C}_{n}^{m}$=${C}_{n}^{n-m}$ | B． | ${C}_{n}^{m}$=$\frac{{A}_{n}^{m}}{n!}$ | ||
| C． | （n+2）（n+1）${A}_{n}^{m}$=${A}_{n+2}^{m+2}$ | D． | ${C}_{n}^{r}$=${C}_{n-1}^{r-1}$+${C}_{n-1}^{r}$ |
1．某几何体的三视图如图所示，它的表面积为（ ）
| A． | 3+$\frac{π}{4}$ | B． | $\frac{5π}{4}$ | C． | $\frac{7π}{8}$ | D． | π |
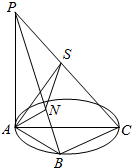如图，AC为圆O的直径，B为圆周上不与点A、C重合的点，PA垂直于圆O所在的平面，连结PB、PC、AB、BC，作AN⊥PB，AS⊥PC，连结SN，则图中直角三角形个数为（ ）