题目内容
已知函数f(x)=ax3-
(a+2)x2+6x+b在x=2处取得极值．
（Ⅰ）求a的值及f（x）的单调区间
（Ⅱ）?x∈[0，3]使f（x）＜b2，求b的范围．
| 3 |
| 2 |
（Ⅰ）求a的值及f（x）的单调区间
（Ⅱ）?x∈[0，3]使f（x）＜b2，求b的范围．
考点：利用导数研究函数的单调性,函数在某点取得极值的条件
专题：导数的综合应用
分析：（Ⅰ）根据函数极值和导数之间的关系建立方程f′（2）=0，即可求a的值及f（x）的单调区间
（Ⅱ）（Ⅱ）?x∈[0，3]使f（x）＜b2，等价为fmin（x）＜b2，求出函数的最小值即可得到结论．
（Ⅱ）（Ⅱ）?x∈[0，3]使f（x）＜b2，等价为fmin（x）＜b2，求出函数的最小值即可得到结论．
解答：
解：（Ⅰ）函数的导数f′（x）=3ax2-3（a+2）x+6，
∵函数在x=2处取得极值，
∴f′（2）=12a-6（a+2）+6=0，解得a=1，
∴f′（x）=3x2-9x+6=3（x2-3x+2）=3（x-1）（x-2），
令f′（x）＞0，则x＜1或x＞2，此时函数单调递增，
令f′（x）＜0，则1＜x＜2，此时函数单调递减，
∴f（x）单调增区间（-∞，1）（2+∞），减区间（1，2）．
（Ⅱ）∵f（x）=x3-
x2+6x+b，
由（Ⅰ）知：f（x）的极小值为f（2）=b+2，
f（0）=b，
f(x)极大值=f(1)=b+
，
f(3)=27-
×9+18+b=b+
，
∴函数f（x）的最小值为f（0）=b，
要使（Ⅱ）?x∈[0，3]使f（x）＜b2，
则f(x)min=b＜b2，解得b＜0或b＞1．
∵函数在x=2处取得极值，
∴f′（2）=12a-6（a+2）+6=0，解得a=1，
∴f′（x）=3x2-9x+6=3（x2-3x+2）=3（x-1）（x-2），
令f′（x）＞0，则x＜1或x＞2，此时函数单调递增，
令f′（x）＜0，则1＜x＜2，此时函数单调递减，
∴f（x）单调增区间（-∞，1）（2+∞），减区间（1，2）．
（Ⅱ）∵f（x）=x3-
| 9 |
| 2 |
由（Ⅰ）知：f（x）的极小值为f（2）=b+2，
f（0）=b，
f(x)极大值=f(1)=b+
| 5 |
| 2 |
f(3)=27-
| 9 |
| 2 |
| 9 |
| 2 |
∴函数f（x）的最小值为f（0）=b，
要使（Ⅱ）?x∈[0，3]使f（x）＜b2，
则f(x)min=b＜b2，解得b＜0或b＞1．
点评：本题主要考查导数的应用，根据函数极值和导数之间的关系，求出a是解决本题的关键．要求熟练掌握导数的应用．
练习册系列答案
相关题目
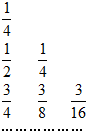下表给出一个“三角形数阵”（如图），已知每一列的数成等差数列，从第三行起每一行的公比都相等，记第i行第j列的数为aij（i≥j，i，j∈N*）．